Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Z_L=80\Omega\)
\(Z_C=100\Omega\)
Áp dụng điều kiện vuông pha với uRL và um :
\(\tan\varphi_{RL}.\tan\varphi_{m}=-1\)
\(\Rightarrow \dfrac{Z_L}{R}.\dfrac{Z_L-Z_C}{R}=-1\)
\(\Rightarrow \dfrac{80}{R}.\dfrac{80-100}{R}=-1\)
\(\Rightarrow R=40\Omega\)

Đáp án A
Tần số góc biến thiên để ULmaxnên ta có:
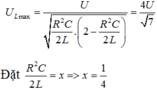
Khi tần số góc là w1thì :
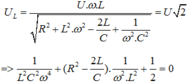
Áp dụng định lý viet phương trình có hai nghiệm phân biệt thỏa mãn:
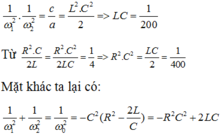
![]()
![]()


Chọn D
Vì từ ω = 1 2 L C => 2ωL = 1 ω C hay 2ZL = ZC
=> ( Z L - Z C ) 2 = Z L 2
⇒ UAM = IZAM = U R 2 + ( Z L - Z C ) 2 R 2 + Z L 2 = U
UAM = U = const

Giải thích: Đáp án B
+ Khi L = L1 và ω = 120π rad/s thì UL có giá trị cực đại nên sử dụng hệ quả khi UL max ta có:
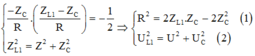
Thay U = 120 V và UC = 40 3 V ta có:
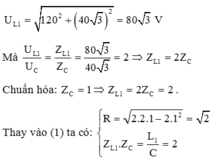
+ Khi L2 = 2L1 thì vẫn thay đổi ω để UL max nên:


Đáp án A
Phương pháp: sử dụng điều kiện cực đai của UL khi tần số góc biến đổi
Cách giải: Tần số góc biến thiên để ULmax nên ta có:
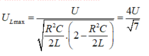
Đặt R 2 C 2 L = x ⇒ x = 1 4 Khi tần số góc là ω 1 thì:

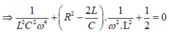
Áp dụng định lý vi et phương trình có hai nghiệm phân biệt thỏa mãn:
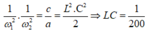
Từ 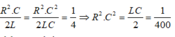
Mặt khác ta lại có:

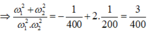
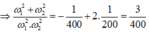
Biết tổng và tích ta tìm ra được

Vậy ω 1 = 10 2

Đáp án D
+ Dòng điện chạy qua mạch RLC có giá trị tức thời phụ thuộc vào thời gian theo quy luật hàm số sin hoặc cosin

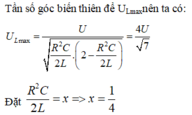
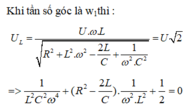
Áp dụng định lý viet phương trình có hai nghiệm phân biệt thỏa mãn
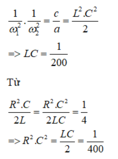
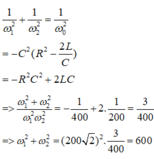
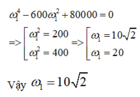
Đáp án A

Đáp án B
+ Hai giá trị của tần số góc cho cùng dòng điện hiệu dụng trong mạch thỏa mãn
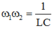
Chọn đáp án C
U L max ⇔ Z L = R 2 + Z C 2 Z C ⇔ ω L = R 2 + 1 ω 2 C 2 1 ω C ⇒ L = C R 2 + 1 ω 2 C