Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

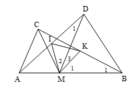
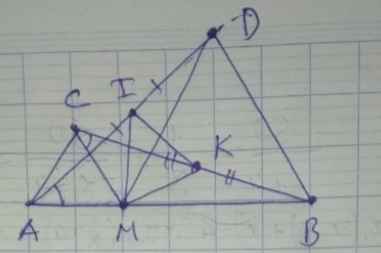
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M

Em tham khảo tại đây nhé:
Câu hỏi của Phạm Thị Thu Trang - Toán lớp 7 - Học toán với OnlineMath

.png)
a) Do AMC và BMD là các tam giác đều nên \(\widehat{AMC}=\widehat{BMD}=60^o\)
\(\Rightarrow\widehat{AMD}=\widehat{CMB}\)
Xét tam giác AMD và tam giác CMB có:
AM = CM
MD = MB
\(\widehat{AMD}=\widehat{CMB}\)
\(\Rightarrow\Delta AMD=\Delta CMB\left(c-g-c\right)\)
\(\Rightarrow AD=BC\)
b) Do \(\Delta AMD=\Delta CMB\Rightarrow\widehat{EAM}=\widehat{FCM}\)
Xét tam giác AEM và tam giác CFM có:
\(\widehat{EAM}=\widehat{FCM}\)
AE = CF (Cùng bằng một nửa AD)
AM = CM
\(\Rightarrow\Delta AEM=\Delta CFM\left(c-g-c\right)\)
\(\Rightarrow ME=MF\)
Ta cũng có ngay \(\Delta EDM=\Delta FBM\left(c-g-c\right)\)
\(\Rightarrow\widehat{EMD}=\widehat{FMB}\)
\(\Rightarrow\widehat{EMF}=\widehat{EMD}+\widehat{DMF}=\widehat{FMB}+\widehat{DMF}=\widehat{DMB}=60^o\)
Xét tam giác MEF có ME = MF nên nó là tam giác cân. Lại có \(\widehat{EMF}=60^o\) nên tam giác MEF là tam giác đều.
A B C M D F E
a) Dễ thấy: ^CMD = 1800 - (^AMC + ^BMD) = 600
Ta có: ^CMB = ^CMD + ^BMD = 1200; ^AMD = ^CMD + ^AMC = 1200
=> ^CMB = ^AMD.
Xét \(\Delta\)MCB và \(\Delta\)MAD có: MC=MA; ^CMB = ^AMD; MB=MD => \(\Delta\)MCB = \(\Delta\)MAD (c.g.c)
=> BC = AD (2 cạnh tương ứng) (đpcm).
b) BC=AD (cmt) => 1/2.BC=1/2.AD => CF=AE
\(\Delta\)MCB = \(\Delta\)MAD (cmt) => ^MCB = ^MAD hay ^MCF = ^MAE
Xét \(\Delta\)MFC và \(\Delta\)MEA có: CF=AE; ^MCF= ^MAE; MC=MA => \(\Delta\)MFC = \(\Delta\)MEA (c.g.c)
=> MF = ME (2 cạnh tương ứng) (1)
Đồng thời ^CMF = ^AME (2 góc tương ứng). Mà ^AME + ^CME = 600
=> ^CMF + ^CME = 600 => ^EMF = 600 (2)
Tù (1) và (2) => \(\Delta\)MEF đều (đpcm).