Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có AM ; AN lần lượt là tiếp tuyến đường tròn(O) với M;N là tiếp điểm
nên ^AMO = ^ANO = 900
Xét tứ giác AMON có ^AMO + ^ANO = 1800
mà 2 góc này đối nhau
Vậy tứ giác AMON nt 1 đường tròn

BE//AM
=>góc MAB=góc EBH=góc MNH
=>B,N,H,E cùng thuộc 1 đường tròn
=>góc ENB=góc EHB=góc MCB
=>EH//MC

a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔAKM và ΔAMI có
góc AMK=góc AIM
góc MAK chung
=>ΔAKM đồng dạng với ΔAMI
=>AK/AM=AM/AI
=>AM^2=AI*AK
Xét ΔABM và ΔAMC có
góc AMB=góc ACM
góc BAM chung
=>ΔABM đồng dạng với ΔAMC
=>AB/AM=AM/AC
=>AM^2=AB*AC=AK*AI

a.
Do MA là tiếp tuyến \(\Rightarrow AM\perp OA\Rightarrow\Delta OAM\) vuông tại A
\(\Rightarrow O,A,M\) cùng thuộc đường tròn đường kính OM
Do \(OK\perp BC\Rightarrow\Delta OKM\) vuông tại K
\(\Rightarrow O,K,M\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow M,A,O,K\) cùng thuộc đường tròn đường kính OM
Hay tứ giác MAOK nội tiếp đường tròn đường kính OM, với tâm là trung điểm J của OM và bán kính \(R=\dfrac{OM}{2}\)
b.
Do \(AI||BC\Rightarrow\widehat{IAK}=\widehat{AKM}\) (so le trong)
Lại có MAOK nội tiếp \(\Rightarrow\widehat{AKM}=\widehat{AOM}\) (cùng chắn cung AM)
\(\Rightarrow\widehat{IAK}=\widehat{AOM}\) (1)
Mà \(\widehat{AOM}+\widehat{AMO}=90^0\) (\(\Delta OAM\) vuông tại A theo c/m câu a)
\(\Rightarrow\widehat{IAK}+\widehat{AMO}=90^0\)
c.
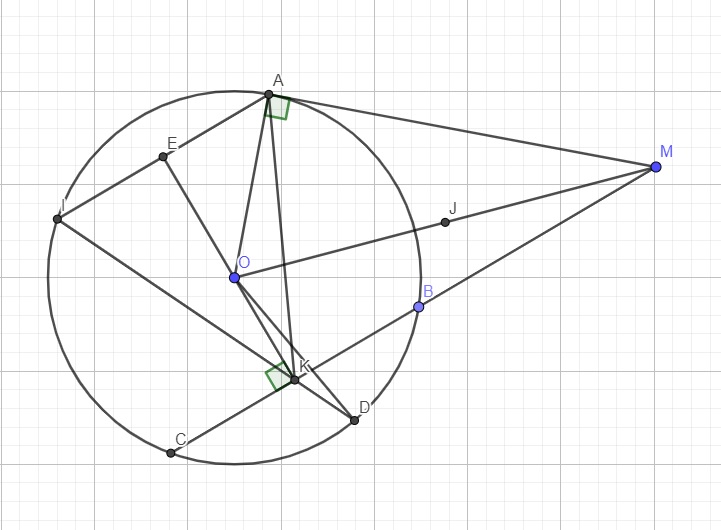
Gọi E là trung điểm AI \(\Rightarrow OE\perp IA\)
Mà \(IA||BC\Rightarrow OE\perp BC\Rightarrow O,E,K\) thẳng hàng
\(\Rightarrow KE\) đồng thời là đường cao và trung tuyến trong tam giác KAI
\(\Rightarrow\Delta KAI\) cân tại K \(\Rightarrow\widehat{AIK}=\widehat{IAK}\) \(\Rightarrow\widehat{AIK}=\widehat{AOM}\) (theo (1))
Mặt khác \(\widehat{AIK}\) và \(\widehat{AOD}\) là góc nội tiếp và góc ở tâm cùng chắn cung AD của (O)
\(\Rightarrow\widehat{AIK}=\dfrac{1}{2}\widehat{AOD}\Rightarrow\widehat{AOM}=\dfrac{1}{2}\left(\widehat{AOM}+\widehat{MOD}\right)\)
\(\Rightarrow\widehat{AOM}=\widehat{MOD}\)
Xét hai tam giác AOM và DOM có:
\(\left\{{}\begin{matrix}OM\text{ chung}\\\widehat{AOM}=\widehat{MOD}\left(cmt\right)\\AO=DO=R\end{matrix}\right.\) \(\Rightarrow\Delta AOM=\Delta DOM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODM}=\widehat{OAM}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến của (O)

a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: ΔOBC cân tại O có OI là trung tuyến
nên OI vuông góc BC
Xét (O) có
AM,AN là tiếp tuyến
=>AM=AN
mà OM=ON
nên OA là trung trực của MN
=>OA vuông góc MN tại H
Xét ΔAHK vuông tại H và ΔAIO vuông tại I có
góc HAK chung
=>ΔAHK đồng dạng vớiΔAIO
=>AH/AI=AK/AO
=>AH*AO=AK*AI=AB*AC