Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành

Bài 1:
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)

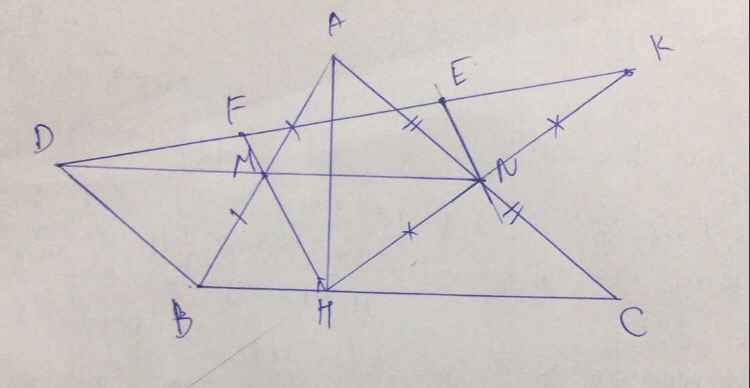
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang
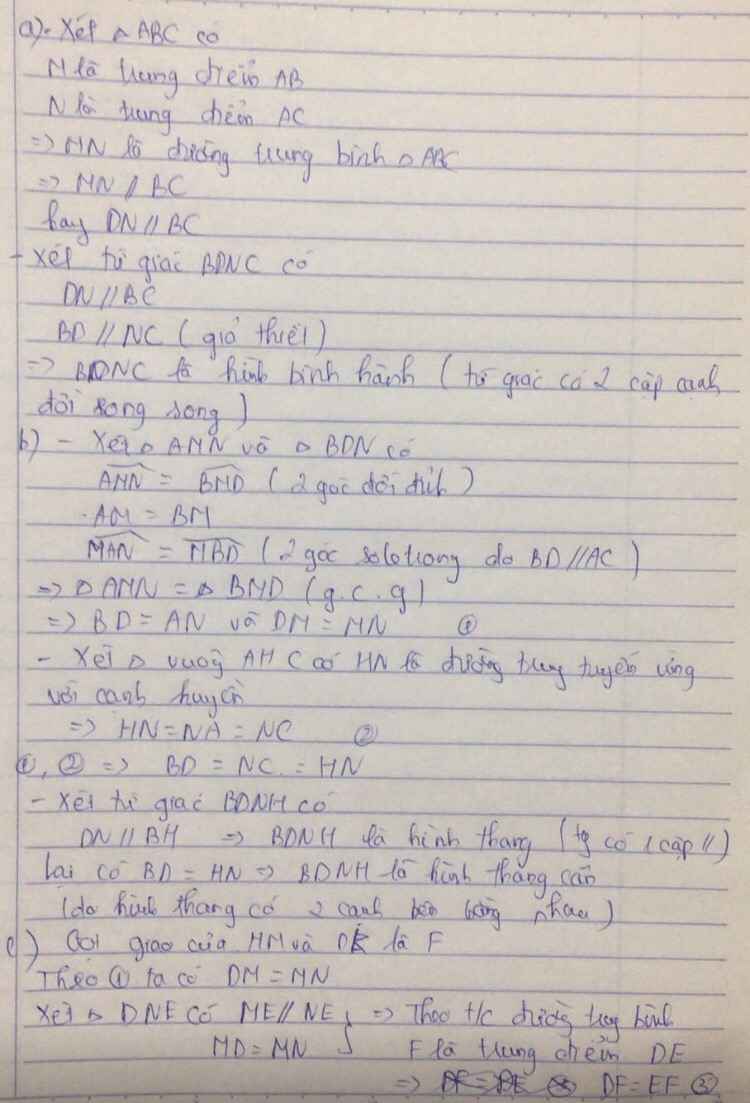
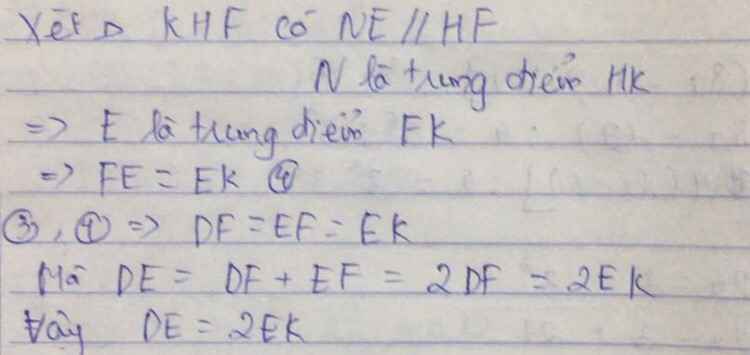
a,
Vì BC=CD(giả thiết)và AC=BC => AC=CD
=> Tam giac CAD cân tại C
=> D=180-C-A=180-(180-BCA)-D
=> 2D=180-180+60=60
=>D=30
=>CAD=C=30
=> A= BAC +CAD= 60+30=90
=> tam giac ABC vuông tại A
b,
Ta có :
AB=BC=6 cm
=> BD= 2BC= 2.6=12(cm);
Vì tam giác ABC đều nên
AH là đường cao cũng là đường trung tuyến
=> HB=HC=1/2 BC=1/2 .6=3(cm)
Xét tam giac ABD có: A=90
=> theo định lý Pytago, ta có:
AD2 =AB2 +BD2
=> AD= /(AB2+BD2)= /(62 + (3+6)2) = 10.82(cm)
=> AM=1/2 AD =1/2. 10,82=5,4 (cm)
Vì tam giác CAD cân nên
CM là dường trung tuyến cũng là dường cao ứng với cạnh đáy AD
Xét tam giác AMC có AMC=90
=> theo định lí Pytago ta có: CM=2.6 (cm)
chu vi tứ giác ABCM là :
AB+BC+CM+AM= 6+6+2.6+5.4=20(cm)
c,
Xét tam giác ACD co
N là trung điểm của AC
M là trung điểm của AD
=> NM là đường trung bình của tam giác ACD
=> MN//CD hayMN//CH (1)
MN=1/2 CD mà CH=1/2 CD => MN=CH (2)
Từ (1)và (2) => tứ giác MNHC là hình bình hành
Mình góp ý nha ý a đúng rồi nhưng ý b và c chưa đúng.
b, Bạn ấy sai ở chỗ \(AD^2=AB^2+BD^2\) (tam giác ABD vuông tại A chứ ko phải vuông tại B)
Gợi ý: -Tính \(HB=HC=3cm\)
-Tính \(AH=\sqrt{27}\left(cm\right)\)(định lí Pitago vào tam giác AHB)
-C/m \(\Delta ACD\)cân tại C mà AM là trung tuyến nên AM là đường cao
-Tính \(\widehat{HAC}=\widehat{MAC}=30^0\)
- \(\Delta HAC=\Delta MAC\left(ch-gn\right)\Rightarrow\hept{\begin{cases}AH=AM=\sqrt{27}\left(cm\right)\\HC=MC=3cm\end{cases}}\)
Chu vi tứ giác ABCM là: \(AB+BC+CM+AM=6+6+3+\sqrt{27}=15+\sqrt{27}\left(cm\right)\)
c,MNHC chỉ là hình thang.
Ở đoạn gần cuối bạn ấy ghi \(HC=\frac{1}{2}CD\) là sai vì \(HC=\frac{1}{2}BC\) chứ ko bằng 1/2 CD
Còn MN//HC thì đúng rồi. Chúc bạn học tốt.