Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

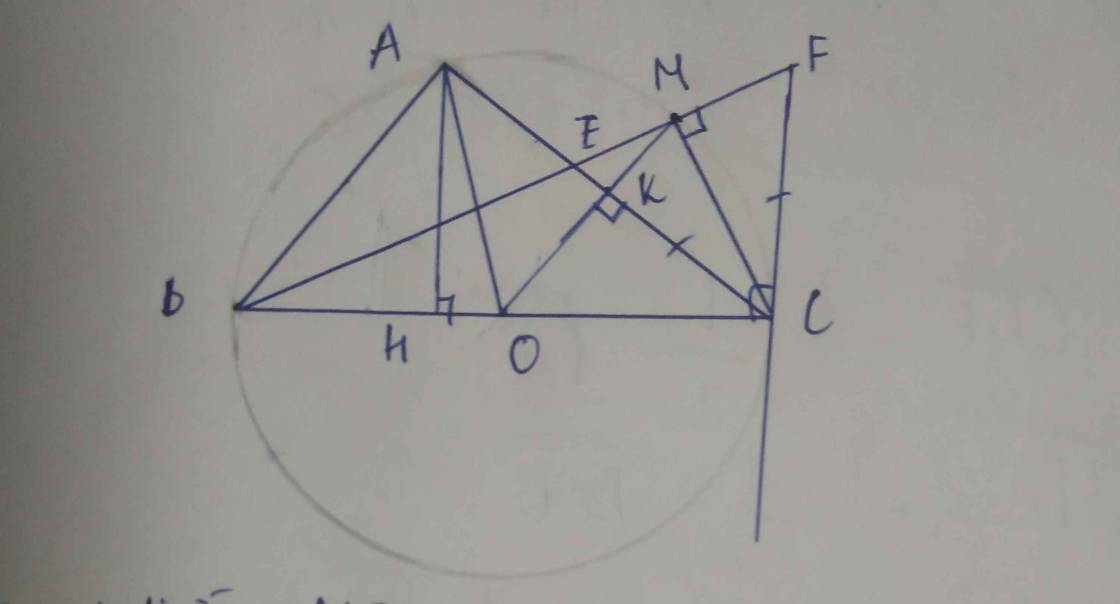
1: M là điểm chính giữa của cung AC
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
góc AHO+góc AKO=180 độ
=>AHOK nội tiếp
3: Gọi G là trung điểm của AB
ΔOAB cân tại O
mà OG là trung tuyến
nên OG là trung trực của AB
=>OH là một phần đường kính của đường tròn ngoại tiếp ΔOAB
Xet ΔABC co BH/BA=BO/BC
nên OH//AC
=>OH vuông góc OM
=>OM tiếp xúc với đường tròn ngoại tiêp ΔABC

a) từ E kẻ đường kính ED' => H thuộc ED' => góc EAD'=90( góc nt chắn nửa đường tròn)
mặt khác ta lại có góc EAD=90( E thuộc AC, D thuộc AB) => D trùng D' => 3 điểm E,H,D thẳng hàng
b) (H): HA=HD=R => tam giác AHD cân => góc HAD=góc HDA
AH là đường cao => góc AHB =90 => góc HAB=góc ACB( cùng phụ góc ABC) hay góc HAD=góc ACB
=> góc HDA=ACB
xét tam giác ABC và tam giác AED: góc A chung, góc HDA=góc ACB => 2 tam giác đồng dạng theo trường hợp g.g
c) tam giác AHM vuông tại H => MH=\(\sqrt{AM^2-AH^2}=\sqrt{5^2-4,8}^2=1,4\)
Tam giác ABC vuông , AM là trung tuyến => MA=MB=MC=5
=> BC=10cm; HC=MC+MH=5+1,4=6,4
HB=MB-MH=5-1,4=3,6
áp dụng hệ thức lượng:
\(AC=\sqrt{BC.HC}=\sqrt{10.6,4}=8\);
từ H kẻ HK vuông góc AB tại K => HK//AC => tam giác ACB đồng dạng tam giác KHB =>\(\frac{KH}{AC}=\frac{HB}{BC}\Leftrightarrow KH=\frac{3,6.8}{10}=2,88\)
S tứ giác AHDM=S MHA+ S AHD
S MHA=1/2 .AH.MH=1/2 .4,8.1,4=3,36.
(H): HA=HD=> HD=5. tam giác AKD vuông tại K=> KD=\(\sqrt{HD^2-HK^2}=\sqrt{5^2-2,88^2}=\sqrt{16,7056}\)
Tam giac AHD cân => HK là đường cao đồng thời là trung tuyến => AD=2KD=\(2\sqrt{16,7056}\)
=> S AHD=1/2.HK.AD=\(\frac{1}{2}.2,88.2\sqrt{16,7056}\)
rồi cộng 2 cái vào là xong nha.
đúng nha. mình làm bài này vừa dài vừa mệt

a: MA=MC
OA=OC
=>OM là trung trực của AC
=>OM vuông góc AC tại K
góc AHO+góc AKO=180 độ
=>AHOK nội tiếp
b:
góc BMC=1/2*sđ cung BC=90 độ
=>CM vuông góc BC
góc CFE+góc CBM=90 độ
góc CBM+góc MCB=90 độ
=>góc CFE=góc MCB
góc CEM=1/2(sđ cung CM+sđ cung BA)
=1/2(sđ cung AM+sđ cung AB)
=1/2*sđ cung MB
=góc MCB
=>góc CEF=góc CFE
=>ΔCEF cân tại C

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)


Lời giải:
Xét $(H)$ có \(\widehat{DAE}=90^0\Rightarrow \widehat{DHE}=2\widehat{DAE}=180^0\) (góc ở tâm thì gấp đôi góc nội tiếp cùng chắn 1 cung)
\(\Rightarrow D,H,E\) thẳng hàng.
Do đó:
\(\widehat{BDE}=\widehat{ADE}=\widehat{ADH}=\widehat{HAD}\) (do tam giác AHD cân tại H)
\(=\widehat{HAB}=90^0-\widehat{HAC}=\widehat{HCA}=\widehat{BCE}\)
Vậy \(\widehat{BDE}=\widehat{BCE}\), mà 2 góc này cùng nhìn cạnh $BE$ nên $BECD$ là tứ giác nội tiếp (đpcm)
Hình vẽ:
P/s: Điểm M là điểm không cần thiết.