Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

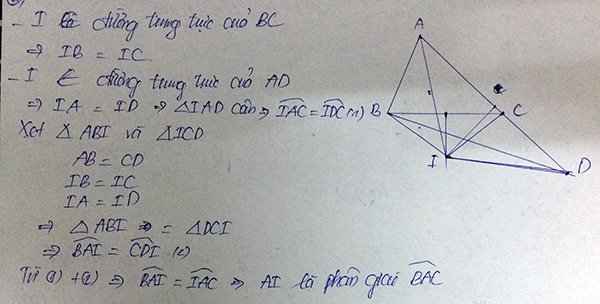
Xét ΔAID=ΔBIC có:
IA=IB(gt)
IC=ID(gt)
góc AID=góc CIB
Vậy ΔAID=ΔBIC (c-g-c)
=>góc IBC=góc DAB (2 góc tương ứng)
Mà góc IBC và góc DAB là hai góc so le trong
=>AD//BC (dấu hiệu nhận biết)
Vì ΔAID=ΔBIC
=>AD=CB (2 cạnh tương ứng)
Mà M,N lần lượt là trung điểm của AD và BC=>AM=NB
Xét t/g AIM và t/g BIN có :
AI=IB(gt)
NB=AM(cmt)
góc MAI=góc IBN (cmt)
Vậy t/g AIM=t/g BIN (c-g-c)
=>MI=NI (2 cạnh tương ứng)
Vì t/g AIM=t/g BIN =>góc AIM=góc NIB (2 góc tương ứng)
Mà góc AIM+góc AIN=180 độ
=>góc NIB+góc AIN=180 độ
=>M,I,N thẳng hàng


a) C/m AH là đường trung tuyến
Có 2 cách để làm:
- Cách 1:
Xét ΔvABH và ΔvACH có:
AB = AC ( ΔABC cân)
\(\widehat{ABH}=\widehat{ACH}\) (ΔABC cân)
Do đó: ΔvABH = ΔvACH (ch-gn)
=> BH = CH (cạnh tương ứng)
Vậy AH là đường trung tuyến của ΔABC
- Cách 2:
Ta có: AH ⊥ BC (gt)
=> AH là đường cao của ΔABC
Mà: ΔABC cân
=> AH cũng là đường trung tuyến của ΔABC
b) So sánh AC và AD
Ta có:
HC là hình chiếu của AC
HD là hình chiếu của AD
Mà: HC > HD (C nằm giữa HD)
Vậy AC < AD
c) Hơi khó :v

bạn ơi sao cái bài 1 hồi nãy bạn giải dùm mày bạn chưa vẽ hình cho mình vậy với gt , kl nữa

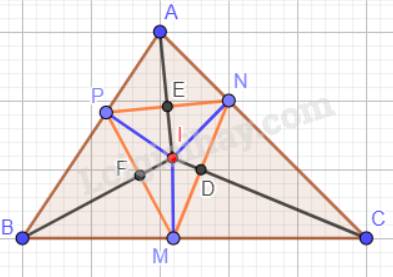
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.