Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tìm phần tử có giá trị bằng 34 trong dãy A = {0, 4, 9, 10, 12, 14, 17, 18, 20, 31, 34, 67} bằng thuật toán tìm kiếm tuần tự, ta sẽ duyệt qua từng phần tử của dãy cho đến khi tìm thấy phần tử cần tìm.
Vì phần tử 34 nằm ở vị trí thứ 11 trong dãy, nên số lần duyệt cần thực hiện để tìm ra phần tử này là 11 lần, bao gồm cả phần tử 34.
Vậy, cần duyệt qua 11 phần tử để tìm ra phần tử có giá trị bằng 34 trong dãy A

Trong trường hợp này, chúng ta cần tìm phần tử có giá trị là 47 trong dãy A = [1, 91, 45, 23, 67, 9, 10, 47, 90, 46, 86]. Ta sẽ thực hiện duyệt từng phần tử trong dãy này để tìm kiếm phần tử có giá trị là 47.
Dãy A có tổng cộng 11 phần tử, và trong trường hợp xấu nhất, phần tử cần tìm là phần tử cuối cùng của dãy. Vì vậy, trong trường hợp xấu nhất, ta cần duyệt qua toàn bộ dãy A để tìm thấy phần tử có giá trị là 47.
Vậy, số lần duyệt cần thực hiện là 7 lần.

def timTatCaGiaTri(a, x):
danhSach = [] # Khởi tạo danh sách rỗng để lưu trữ các phần tử tìm thấy
for i in range(len(a)):
if a[i] == x:
danhSach.append(i) # Nếu phần tử được duyệt là phần tử cần tìm, thêm chỉ số của nó vào danh sách
return danhSach # Trả về danh sách chứa các chỉ số của các phần tử bằng giá trị cần tìm

a)
import time
def linear_search(arr, x):
"""
Tìm kiếm tuyến tính trong dãy arr để tìm giá trị x.
Trả về vị trí của x trong dãy nếu x được tìm thấy, -1 nếu không tìm thấy.
"""
n = len(arr)
for i in range(n):
if arr[i] == x:
return i
return -1
# Dãy số A
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 11]
# Phần tử cần tìm kiếm
C = 9
# Bắt đầu đo thời gian
start_time = time.perf_counter()
# Tìm kiếm phần tử C trong dãy A
result = linear_search(A, C)
# Kết thúc đo thời gian
end_time = time.perf_counter()
if result != -1:
print(f"Phần tử {C} được tìm thấy tại vị trí {result} trong dãy A.")
else:
print(f"Phần tử {C} không có trong dãy A.")
print(f"Thời gian thực hiện thuật toán: {end_time - start_time} giây.")
b)
import time
def binary_search(arr, x):
"""
Tìm kiếm nhị phân trong dãy arr để tìm giá trị x.
Trả về vị trí của x trong dãy nếu x được tìm thấy, -1 nếu không tìm thấy.
"""
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == x:
return mid
elif arr[mid] < x:
left = mid + 1
else:
right = mid - 1
return -1
# Dãy số A đã được sắp xếp
A = [0, 1, 3, 5, 7, 9, 10, 11, 13, 16]
# Phần tử cần tìm kiếm
C = 9
# Bắt đầu đo thời gian
start_time = time.perf_counter()
# Tìm kiếm phần tử C trong dãy A bằng thuật toán tìm kiếm nhị phân
result = binary_search(A, C)
# Kết thúc đo thời gian
end_time = time.perf_counter()
if result != -1:
print(f"Phần tử {C} được tìm thấy tại vị trí {result} trong dãy A.")
else:
print(f"Phần tử {C} không có trong dãy A.")
print(f"Thời gian thực hiện thuật toán: {end_time - start_time} giây.")
-Thời gian thực hiện ở câu a là 8.99999,thời gian thực hiện ở câu b là 6,49999 giây.

Em có thể thực hiện như sau:
- Duyệt qua từng phần tử của dãy từ đầu đến cuối.
- So sánh hai phần tử liền kề, nếu phần tử sau lớn hơn phần tử trước thì hoán đổi chúng.
- Tiếp tục duyệt qua các phần tử còn lại cho đến khi không còn phần tử nào cần hoán đổi.
- Lặp lại quá trình trên cho đến khi toàn bộ dãy được sắp xếp.
Hoặc:
-Duyệt qua từng phần tử của dãy từ đầu đến cuối.
-Lưu giá trị của phần tử hiện tại vào biến tạm thời.
-So sánh phần tử hiện tại với các phần tử bên trái, nếu phần tử nào lớn hơn phần tử hiện tại thì dời chúng sang phải một vị trí.
-Chèn giá trị của phần tử hiện tại vào vị trí đúng sau khi dời các phần tử.
-Tăng vị trí phần tử hiện tại lên 1 và lặp lại quá trình trên cho đến khi toàn bộ dãy được sắp xếp.

a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:
- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5
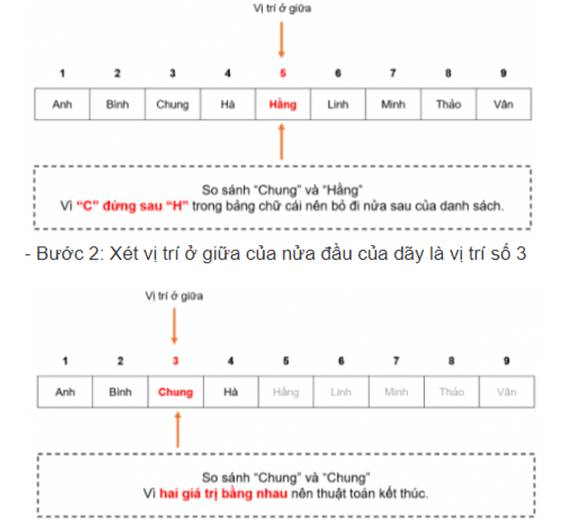
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.
b) Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.
Thuật toán tuần tự
- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.
- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.
- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.

Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.
Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.

uses crt;
var a:array[1..1000]of integer;
i,n,k,dem:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap k='); readln(k);
for i:=1 to n do
if a[i]=k then
begin
writeln(i);
break;
end;
dem:=0;
for i:=1 to n do
if a[i]=k then inc(dem);
if dem>0 then writeln('Co ',dem,' phan tu bang ',k)
else writeln('Khong co phan tu nao bang ',k);
readln;
end.

1.Thuật toán tìm kiếm tuần tự:
- Độ phức tạp thời gian của thuật toán tìm kiếm tuần tự là O(n)
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = 1 giây * (106 us / phép tính) = 106
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = 1 phút * (60 giây / phút) * (106us / phép tính) = 6 * 107
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = 1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính) = 3.6 * 109
2.Thuật toán sắp xếp chèn:
- Độ phức tạp thời gian của thuật toán sắp xếp chèn là O(102
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = sqrt(1 giây * (106us / phép tính)) =103
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 6 * 104
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
3. Thuật toán sắp xếp chọn:
- Độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2)
- Giá trị lớn nhất của n là: n = sqrt(1 giây * (106us / phép tính)) = 1000.
Thời gian thực thi là 1 phút:
Giá trị lớn nhất của n là: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 60000.
Thời gian thực thi là 1 giờ:
Giá trị lớn nhất của n là: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
Với thuật toán tìm kiếm tuần tự, cần duyệt 10 phần tử để tìm ra phần từ có giá trị bằng 34.