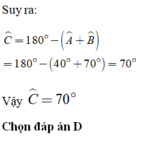Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có ΔABC = ΔDEF
Suy ra: AB = DE; AC = DF; BC = EF
∠A = ∠D ; ∠B = ∠E ; ∠C = ∠F

Ta có: Δ A B C = Δ H I K ⇒ AB = HI = 5 cm BC = IK = 7 cm AC = HK
Chu vi tam giác ABC là: AB + BC + AC = 20 cm
Suy ra AC = 20 – AB – BC = 20 – 5 – 7 = 8 cm
Vậy AC = 8 cm.
Chọn đáp án D

Lời giải:
Kẻ $MT\perp AC$
Xét tam giác $ABH$ và $AMH$ có:
$\widehat{BAH}=\widehat{MAH}$
$\widehat{AHB}=\widehat{AHM}$
$AH$ chung
$\Rightarrow \triangle ABH=\triangle AMH$ (c.g.c)
$\Rightarrow BH=HM$
Tương tự ta cũng cm được: $\triangle AMH=\triangle AMT$ (ch-gn)
$\Rightarrow HM=MT$
Do đó: $BH=HM=MT (=\frac{1}{2}BM$)
Mà $BM=MC$ nên $MT=\frac{1}{2}MC$
Xét tam giác $MTC$ vuông tại $T$ có $MT=\frac{1}{2}MC$ nên $\widehat{C}=30^0$
Xét tam giác $AHC$ vuông tại $H$ có $\widehat{C}=30^0$ nên $\widehat{HAC}=60^0$
Mà $\widehat{HAC}=\frac{2}{3}\widehat{BAC}$ nên $\widehat{BAC}=90^0$
Còn lại $\widehat{B}=60^0$

Bạn tham khảo lời giải tại đây:
https://hoc24.vn/cau-hoi/cho-dabc-ke-ahbc-m-la-trung-diem-cua-bc-biet-aham-chia-goc-bac-thanh-ba-goc-bang-nhau-tinh-cac-goc-cua-dabc.552082525880

Tam giác EFD là tam giác vuông vì \(20^2=12^2+16^2\)

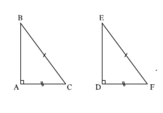
- Bổ sung AB =DE thì ΔABC = ΔDEF (c.g.c)
- Hoặc Bổ sung góc C = góc F (2 tam giác bằng nhau theo trường hợp g.c.g)
- Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)