Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
DO đó: ΔABD=ΔAED
Suy ra: DB=DE
b: Để ΔADB=ΔADC thì AB=AC
c: Để DE\(\perp\)AC thì \(\widehat{ABC}=90^0\)

A B C E D M H
a) Xét \(\Delta ADB\)và \(\Delta AEC\), có :
góc A chung
góc AEC = góc ADB = 90o
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ADB=\Delta AEC\left(ch-gn\right)\)
b) Nối A với H
Xét \(\Delta AEH\) và \(\Delta ADH\) , có :
AH chung
góc AEH = góc ADH = 900
AC = AD ( \(\Delta ADB=\Delta AEC\) )
=> \(\Delta AEH=\Delta ADH\left(ch-cgv\right)\)
=> HE = HD ( 2 cạnh t/ứ)
c) Ta có : H là giao của 2 đường cao BD và CE trong \(\Delta ABC\)
=> H là trực tâm của \(\Delta ABC\)
Ta lại có : \(AM\perp BC\)
=> AM là đường cao thứ ba của \(\Delta ABC\)
=> AM đi qua H ( trực tâm )
d) Ta có : \(\Delta ADB=\Delta AEC\) (cmt)
=> BD = CE ; AE = AD
Áp dụng định lí Py-ta-go , ta có :
AB2= AD2 + BD2 = AE2 + EC2 ( vì BD = EC ; AE = AD )
AC2 = EA2 + EC2
BC2 = EC2 + BE2
Cộng vế với vế của ba đẳng thức trên , ta được :
AB2 + AC2 + BC2 = 3EC2 + 2EA2 + EB2 => đpcm

c, Vì H là giao của 2 đường cao BD, CE trong tam giác ABC
=> H là trực tâm của tam giác ABC
Mà AM vuông góc với BC
=> AM là đường cao thứ 3 của tam giác ABC
=> AM đi qua trực tâm H
d. Có tam giác ABD = tam giác ACE ( cạnh huyền-góc vuông)
=> AD = AE ; BD = CE
Áp dụng định lí Pi-ta-go có:
\(AB^2=AD^2+BD^2=AE^2+EC^2\) ( VÌ AD = AE ; BD = EC )
\(AC^2=EA^2+EC^2\)
\(BC^2=EC^2+BE^2\)
Cộng vế với vế 3 đẳng thức trên ta được:
\(AB^2+AC^2+BC^2=3EC^2+2EA^2+EB^2\) ( đpcm)

cảm ơn vì câu trả lời của bạn bạn có thể giúp mình câu hỏi dưới đây ko ạ cảm ơn bạn rất nhiều

Câu 2:
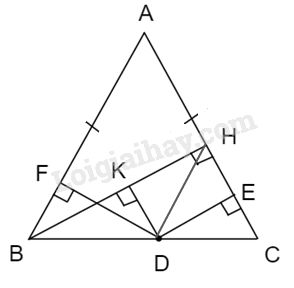
Kẻ \(DK\perp BH.\)
Mà \(BH\perp AC\left(gt\right)\)
=> \(DK\) // \(AC\) (từ vuông góc đến song song).
Hay \(DK\) // \(HC.\)
=> \(\widehat{KDB}=\widehat{HCD}\) (vì 2 góc đồng vị).
+ Vì \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{HCD}.\)
Mà \(\widehat{KDB}=\widehat{HCD}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{KDB}.\)
Xét 2 \(\Delta\) vuông \(BFD\) và \(DKB\) có:
\(\widehat{BFD}=\widehat{DKB}=90^0\)
Cạnh BD chung
\(\widehat{FBD}=\widehat{KDB}\left(cmt\right)\)
=> \(\Delta BFD=\Delta DKB\) (cạnh huyền - góc nhọn).
=> \(DF=BK\) (2 cạnh tương ứng) (1).
Nối D với H.
+ Vì \(DK\) // \(AC\left(cmt\right)\)
=> \(DK\) // \(EH.\)
=> \(\widehat{KDH}=\widehat{EHD}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) vuông \(DEH\) và \(HKD\) có:
\(\widehat{DEH}=\widehat{HKD}=90^0\)
Cạnh DH chung
\(\widehat{EHD}=\widehat{KDH}\left(cmt\right)\)
=> \(\Delta DEH=\Delta HKD\) (cạnh huyền - góc nhọn).
=> \(DE=HK\) (2 cạnh tương ứng) (2).
Từ (1) và (2) => \(DF+DE=BK+HK.\)
Mà \(BK+HK=BH\)
=> \(DF+DE=BH\left(đpcm\right).\)
Chúc bạn học tốt!
Hình vẽ:
A B C E D 1 2
Giải:
a) Xét tam giác ABD và tam giác AED, ta có:
\(\widehat{A_1}=\widehat{A_2}\) (AD là tia phân giác của góc A)
AD là cạnh chung
\(AB=AE\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta AED\left(c.g.c\right)\)
\(\Rightarrow DB=DE\) (Hai cạnh tương ứng)
\(\Rightarrowđpcm\)
b) Ta có:
\(AB=AE\)
Mà \(E\in AC\)
Nên để \(\Delta ABD=\Delta ADC\) thì phải thêm điều kiện \(AB=AC\)
Hay nói cách khác theo hình vẽ là \(C\equiv E\).
c) Để \(DE\perp AC\)
\(\Leftrightarrow\widehat{AED}=90^0\)
Mà \(\widehat{AED}=\widehat{ABD}\) ( \(\Delta ABD=\Delta AED\))
Nên để \(DE\perp AC\) thì phải thêm điều kiện \(\widehat{ABD}=90^0\).
Chúc bạn học tốt!