Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`
\(P\left(x\right)=4x+3x^2+x^2+1-5x-2x\\ =\left(3x^2+x^2\right)+\left(4x-5x-2x\right)+1\\ =4x^2-3x+1\\ Q\left(x\right)=3x+x+7-5x^2+5x-11\\ =-5x^2+\left(3x+x+5x\right)+\left(7-11\right)\\ =-5x^2+9x-4\)
`b)`
Đa thức `P(x)` có :
Bậc `2`
Đa thức `Q(x)` có :
Bậc `2`
`c)`
\(P\left(x\right)+Q\left(x\right)=\left(4x^2-3x+1\right)+\left(-5x^2+9x-4\right)\\ =4x^2-3x+1-6x^2+9x-4\\ =\left(4x^2-5x^2\right)-\left(3x-9x\right)+\left(1-4\right)\\ =-x^2+6x-3\)
a: P(x)=4x^2+4x+1-7x=4x^2-3x+1
Q(x)=-5x^2+9x-4
b: P(x) có bậc 2
Q(x) có bậc 2
c: P(x)+Q(x)=4x^2-3x+1-5x^2+9x-4=-x^2+6x-3

a: A(x)=3/4x^3+5/4x^3+4x^2+7x^2+3/5x-8/5x-1+4
=2x^3+11x^2-x+3
b: Bậc là 3
Hệ số cao nhất là 2
c: C(x)=2x^3+12x^2-3x+3-2x^3-11x^2+x-3
=x^2-2x
C(X)=0
=>x=0 hoặc x=2

a) \(M\left(x\right)=-2x^5+5x^2+7x^4-5x+8+2x^5-7x^4-4x^2+6\)
\(=\left(-2x^5+2x^5\right)+\left(7x^4-7x^4\right)+\left(5x^2-4x^2\right)-9x+\left(8+6\right)\)
\(=x^2-9x+14\)
\(N\left(x\right)=7x^7+x^6-5x^3+2x^2-7x^7+5x^3+3\)
\(=\left(7x^7-7x^7\right)+x^6-\left(5x^3-5x^3\right)+2x^2+3\)
\(=x^6+2x^2+3\)
b) Đa thức M(x) có hệ số cao nhất là 1
hệ số tự do là 14
bậc 2
Đa thức N(x) có hệ số cao nhất là 1
hệ số tự do là 3
bậc 6

a, \(A\left(x\right)+4x^3-x=-5x^2-2x^3+5+3x^2+2x\\ \Leftrightarrow A\left(x\right)=-5x^2-2x^3+5+3x^2+2x-4x^3+x=\left(-2x^3-4x^3\right)+\left(-5x^2+3x^2\right)+\left(2x+x\right)+5\\ =-6x^3-2x^2+3x+5\)
b, \(B\left(x\right)=A\left(x\right):\left(x-1\right)=\left(-6x^3-2x^2+3x+5\right):\left(x-1\right)=-6x^2-8x-5\)
Thay \(x=-1\) vào \(B\left(x\right)\)
\(\Rightarrow-6.\left(-1\right)^2-8\left(-1\right)-5=-3\ne0\)
\(\Rightarrow x=-1\) không là nghiệm của B(x)

a: \(Q\left(x\right)=-5x^6+2x^4+4x^3-4x-1\)
b: \(Q\left(x\right)=-5x^6+2x^4+4x^3-4x-1\)

a: A(x)=3x^5+x^4-x^2+x
B(x)=3x^5-x^4+x^2+x-2
b: M(x)=B(x)-A(x)
=3x^5-x^4+x^2+x-2-3x^5-x^4+x^2-x
=-2x^4+2x^2+2x-2

1: A(x)=5x^4+4x^4+x^2+x^2-x+3
=9x^4+2x^2-x+3
B(x)=-8x^4-x^3-2x^2+3
2: A(x)+B(x)
=9x^4+2x^2-x+3-8x^4-x^3-2x^2+3
=x^4-x^3-x+6
A(x)-B(x)
=9x^4+2x^2-x+3+8x^4+x^3+2x^2-3
=17x^4+x^3+4x^2-x
bậc của A(x)-B(x) là 4
3: P(x)=x^4-x^3-x+6-x^4+x^3=-x+6
P(6)=-6+6=0
=>x=6 là nghiệm của P(x)

`a,`
`Q(x)=`\(-3x^4+4x^3+2x^2+\)\(\dfrac{2}{3}-3x-2x^4-4x^3+8x^4+1+3x\)
`=(-3x^4-2x^4+8x^4)+(4x^3-4x^3)+2x^2+(-3x+3x)+(2/3+1)`
`= 3x^4+2x^2+5/3`
`b,`
Bậc của đa thức: `4`
Hệ số cao nhất: `3`
Hệ số tự do: `5/3`
`c,`
Đặt `3x^4+2x^2+5/3=0`
Vì \(\left\{{}\begin{matrix}x^4\ge0\rightarrow3x^4\ge0\\x^2\ge0\rightarrow2x^2\ge0\end{matrix}\right.\)
`-> 3x^4+2x^2+5/3`\(>0\)
`->` Đa thức `Q(x)` vô nghiệm.
`@`\(\text{dn inactive.}\)

a) \(A\left(x\right)=3x^3-4x^4-2x^3+4x^4-5x+3\)
\(\Rightarrow A\left(x\right)=-4x^4+4x^4+3x^3-2x^3-5x+3\)
\(\Rightarrow A\left(x\right)=x^3-5x+3\)
\(B\left(x\right)=5x^3-4x^2-5x^3-4x^2-5x-3\)
\(\Rightarrow B\left(x\right)=5x^3-5x^3-4x^2-4x^2-5x-3\)
\(\Rightarrow B\left(x\right)=-8x^2-5x-3\)
b) \(A\left(x\right)+B\left(x\right)=x^3-5x+3+\left(-8x^2-5x-3\right)\)
\(\Rightarrow A\left(x\right)+B\left(x\right)=x^3-5x+3-8x^2-5x-3\)
\(\Rightarrow A\left(x\right)+B\left(x\right)=x^3-8x^2-5x-5x+3-3\)
\(\Rightarrow A\left(x\right)+B\left(x\right)=x^3-8x^2-10x\)
\(A\left(x\right)-B\left(x\right)=x^3-5x+3-\left(-8x^2-5x-3\right)\)
\(\Rightarrow A\left(x\right)-B\left(x\right)=x^3-5x+3+8x^2+5x+3\)
\(\Rightarrow A\left(x\right)-B\left(x\right)=x^3+8x^2-5x+5x+3+3\)
\(\Rightarrow A\left(x\right)-B\left(x\right)=x^3+8x^2+6\)
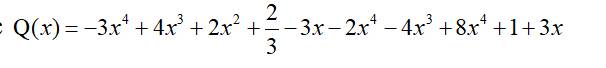

a: B(x)=-4x^3+x^2-3x+2024
b: Bậc 3