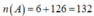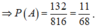Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu \(\Omega\) là tập hợp tất cả các cách chọn ngẫu nhiên 4 đỉnh trong 12 đỉnh
Ta có \(n\left(\Omega\right)=C_{12}^4=495\)
Gọi A là biến cố : 4 đỉnh được chọn tạo thành một hình chữ nhật"
Gọi đường chéo của đa giác đều \(A_1A_2A_3...A_{12}\) đi qua tâm đường tròn (O) là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn.
Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 điểm \(A_1,A_2,A_3,...A_{12}\) có các đường chéo là 2 đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhâtk.
Do đó, số hình chữ nhật được tạo thành là : \(n\left(A\right)=C_6^2=15\)
Vậy xác suất cần tính là \(P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega\right)}=\frac{15}{495}=\frac{1}{33}\)

Tất cả các cạnh của tứ giác là đường chéo khi 4 đỉnh đó ko có 2 đỉnh nào liền kề nhau.
Cố định một đỉnh, có n cách chọn
Chọn đỉnh thứ 2 cách đỉnh thứ nhất \(x_1\) đỉnh, đỉnh thứ 3 cách đỉnh 2 \(x_2\) ; đỉnh thứ 4 cách đỉnh thứ 3 \(x_3\) và cách đỉnh thứ nhất \(x_4\) đỉnh (với \(x_i\ge1\))
\(\Rightarrow x_1+x_2+x_3+x_4=n-4\)
Theo nguyên lý chia kẹo Euler, số nghiệm của pt trên là: \(C_{n-5}^3\)
Vậy số đa giác thỏa mãn là: \(\frac{nC_{n-5}^3}{4}\)
Xác suất: \(P=\frac{nC_{n-5}^3}{4C_n^4}=\frac{30}{91}\) \(\Rightarrow n=15\)

Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)





Chọn D
Số cách chọn 1 tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho là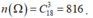
Gọi A là biến cố: “ tam giác được chọn là tam giác cân”.
- TH1: Tam giác được chọn là tam giác đều: có 6 cách.
- TH2: Tam giác được chọn là tam giác cân nhưng không phải tam giác đều:
+ Chọn đỉnh của tam giác cân có 18 cách.
+ Chọn cặp đỉnh còn lại để cùng với đỉnh đã chọn tạo thành đỉnh của tam giác cân (không đều) có 7 cách.
Suy ra số cách chọn tam giác cân nhưng không phải tam giác đều là 18.7 = 126 cách.
Vậy