K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
8 tháng 6 2018
Đáp án D
Phương pháp: Sử dụng công thức 
(giả sử các biểu thức là có nghĩa)
Cách giải: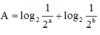 
KT
29 tháng 7 2016
cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)
NM
0
CM
23 tháng 10 2018
Ta có 
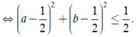
Ta có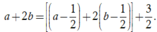 
Áp dụng bất đẳng thức Bunhiacopxky, ta có
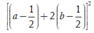
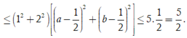
Do đó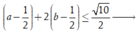 
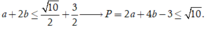
Dấu "x" xảy ra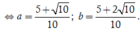 
Chọn C.
Ta thấy (1) là hình tròn tâm 
Ta có 
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung 
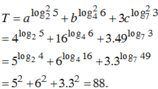
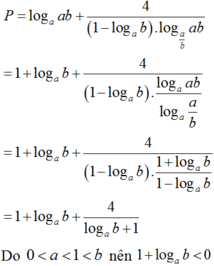
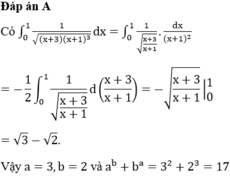
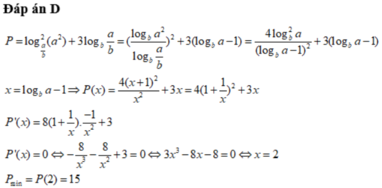
Chọn đáp án A