Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ĐKXĐ: \(a^2-1\ne0\Rightarrow\left(a-1\right)\left(a+1\right)\ne0\Rightarrow a\ne\pm1\)
b) ta có \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{a^2-1}\)
\(=\frac{2a^2+a^2-a-a^2-a}{a^2-1}=\frac{2a^2-2}{a^2-1}=\frac{2\left(a^2-1\right)}{a^2-1}=2\)

ĐK \(x\ne\left\{-2;2\right\}\)
a. Ta có \(A=\left(\frac{x}{\left(x+2\right)\left(x-2\right)}-\frac{2}{x-2}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
\(=\frac{x-2x-4+x-2}{\left(x+2\right)\left(x-2\right)}:\frac{x^2-4+10-x^2}{x+2}=-\frac{6}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{6}=-\frac{1}{x-2}\)
b. Ta có \(\left|x\right|=\frac{1}{2}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
Với \(x=\frac{1}{2}\Rightarrow A=\frac{-1}{\frac{1}{2}-2}=\frac{2}{3}\)
Với \(x=-\frac{1}{2}\Rightarrow A=\frac{-1}{-\frac{1}{2}-2}=\frac{2}{5}\)
c. Để \(A< 0\Rightarrow-\frac{1}{x-2}< 0\Rightarrow x-2>0\Rightarrow x>2\)
Vậy với \(x>2\)thì \(A< 0\)

a) \(x\ne2\) ; \(x\ne-2\)
b) Ta có
\(C=\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}=\frac{x^3}{\left(x-2\right)\left(x+2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3-x.\left(x+2\right)-2.\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\frac{x^2.\left(x-1\right)-4.\left(x-1\right)}{x^2-4}\)
\(=\frac{\left(x-1\right)\left(x^2-4\right)}{x^2-4}=x-1\)
Để C = 0 thì x-1 = 0 =>>> x=1(tm)
c) Để C nhận giá trị dương thì C thuộc Z+ = >>>>>>>> \(x-1\ge0\)=>>> \(x\ge1\)

Ta có: \(\frac{a+b}{c}=\frac{b+c}{a}=\frac{c+a}{b}=\frac{2a+2b+2c}{a+b+c}=2\)
\(\Rightarrow\) a + b = 2c; b + c = 2a; c + a = 2b
\(\Rightarrow\) M = \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)\)
= \(\left(\frac{a+b}{b}\right)\left(\frac{b+c}{c}\right)\left(\frac{a+c}{a}\right)\)
= \(\frac{2c}{b}\times\frac{2a}{c}\times\frac{2b}{a}\)
= 8
Vậy: M = 8.

a) phân thức xác định khi \(x^3+8\ne0\Leftrightarrow x^3\ne-8\Leftrightarrow x\ne-2\)
b)\(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}=\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
d)\(\frac{2}{x+2}=2\Leftrightarrow x+2=1\Leftrightarrow x=-1\)

Ta có: \(n^4+\frac{1}{4}=\frac{4n^4+1}{4}=\left(2n^2+2n+1\right)\left(2n^2-2n+1\right)\)
Áp dụng vào bài toán ta được
\(A=\frac{\frac{3.5}{4}.\frac{13.25}{4}...\frac{1625.1741}{4}}{\frac{5.13}{4}.\frac{25.41}{4}...\frac{1741.1861}{4}}=\frac{3}{1861}\)
Ta có :
\(n^4+\frac{1}{4}=\frac{4n^4+1}{4}\)
\(=\left(2n^2+2n+1\right)\left(2n^2-2n+1\right)\)
áp dụng theo đầubài của bài toán
Ta có :
\(=\frac{\frac{3\times5}{4}\times\frac{13\times25}{4}\times...\times\frac{1625\times1741}{4}}{\frac{5\times13}{4}\times\frac{25\times41}{4}\times...\times\frac{1741\times1861}{4}}=\frac{3}{1861}\)

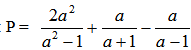

Biểu thức đâu bạn ? :)))
Sau khi ib với Đinh Lan Anh thì \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(a,ĐKXĐ:\hept{\begin{cases}a+1\ne0\\a-1\ne0\end{cases}\Leftrightarrow a\ne\pm1}\)
\(b,P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2+a^2-a-a^2-q}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2-2a}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a\left(a-1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a}{a+1}\)
\(c,P=\frac{2a}{a+1}=\frac{2a+2}{a+1}-\frac{2}{a+1}=2-\frac{2}{a+1}\)
Để \(P\inℤ\)thì \(2-\frac{2}{a+1}\inℤ\)
\(\Leftrightarrow\frac{2}{a+1}\inℤ\)
Mà \(a\inℤ\Rightarrow a+1\inℤ\)
Ta có bảng
Kết hợp ĐKXĐ \(a\ne\pm1\)ta được \(a\in\left\{-3;-2;0\right\}\)
Vậy //////