Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giả sử : \(\frac{mx+m}{\left(m+1\right)x-m+2}>0\)\(,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{m.0+m}{\left(m+1\right).0-m+2}>0\) \(\Rightarrow\frac{m}{2-m}>0\)
\(\Rightarrow0\)\(<\)\(m<\)\(2\)
ngược lại \(0<\)\(m<2\) thì:
\(mx+m>0,\text{∀}x\in\left[0;2\right]\)
\(\left(m+1\right)x\ge0>m-2,\)\(\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\left(m+1\right)x-m+2>0,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{mx+m}{\left(m+1\right)x-m+2}>0,\text{∀}x\in\left[0;2\right]\)
vậy: \(0\)\(<\)\(m<\)\(2\) là kết quả cần tìm

Câu 1 :
Đk: \(x\ge1\)
\(\sqrt{x-1}+\sqrt{2x-1}=5\\ \Leftrightarrow x-1+2\sqrt{\left(x-1\right)\left(2x-1\right)}+2x-1=25\\ \Leftrightarrow2\sqrt{2x^2-3x+1}=27-3x\\ \)
\(\Leftrightarrow\begin{cases}27-3x\ge0\\4\left(2x^2-3x+1\right)=9x^2-162x+729\end{cases}\) \(\Leftrightarrow\begin{cases}x\le9\\x^2-150x+725=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\le9\\x=145hoặcx=5\end{cases}\)
với x= 5 thoản mãn điều kiện, x=145 loại
Vậy \(S=\left\{5\right\}\)

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

1) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)

a) Ta có:
\(M\left(x\right)=A\left(x\right)-2.B\left(x\right)+C\left(x\right)\)
\(=\left(2x^5-4x^3+x^2-2x+2\right)-2.\left(x^5-2x^4+x^2-5x+3\right)+\left(x^4+3x^3+3x^2-8x+4\frac{3}{16}\right)\)
\(=2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-6+x^4+4x^3+3x^2-8x+\frac{67}{16}\)
\(=\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-6+\frac{67}{16}\right)\)
\(=0+5x^4+0+2x^2+0+\frac{3}{16}\)
\(=5x^4+2x^2+\frac{3}{16}\)
b) Thay \(x=-\sqrt{0,25}=-0,5\); ta có:
\(M\left(-0,5\right)=5.\left(-0,5\right)^4+2.\left(-0,5\right)^2+\frac{3}{16}\)
\(=5.0,0625+2.0,25+\frac{3}{16}\)
\(=\frac{5}{16}+\frac{8}{16}+\frac{3}{16}=\frac{16}{16}=1\)
c) Ta có:
\(x^4\ge0\) với mọi x
\(x^2\ge0\) với mọi x
\(\Rightarrow5x^4+2x^2+\frac{3}{16}>0\) với mọi x
Do đó không có x để M(x)=0
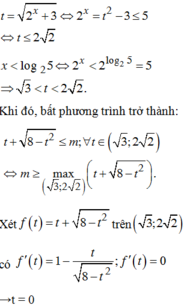
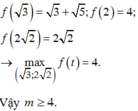
Đáp án B
Điều kiện:
Khi đó
Kết hợp với điều kiên * ⇒ 2 < m ≤ 3 .