Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\overrightarrow{u},\overrightarrow{v}\) theo thứ tự là vec tơ chỉ phương đơn vị của các tia Ox, Oy, tương ứng cùng hướng với các tia Ox, Oy gọi I là tâm của \(\omega\). Chọn O làm gốc vec tơ điểm và với mỗi điểm X của mặt phẳng, ký hiệu \(\overrightarrow{x}\) để chỉ vec tơ \(\overrightarrow{OX}\). Trung trực OA cắt các đường thẳng \(d_1,d_2\) theo thứ tự tại B, C.
Khi đó B, C cố định và do I nằm trên đường thẳng BC nên \(\overrightarrow{i}=\alpha\overrightarrow{b}+\left(1-\alpha\right)\overrightarrow{c}\)
Mặt khác , theo định lí chiếu ta có :
\(\overrightarrow{m}=2\left(\overrightarrow{i}.\overrightarrow{u}\right).\overrightarrow{u}\) và \(\overrightarrow{n}=2\left(\overrightarrow{i}.\overrightarrow{v}\right).\overrightarrow{v}\)
Gọi P là trung điểm MN. Suy ra \(2\overrightarrow{p}=\overrightarrow{m}.\overrightarrow{n}\). Bởi vậy, với \(b=OB,c=OC\) và \(t=\cos<\left(\overrightarrow{u}\overrightarrow{v}\right)\) thì b, c, t là các hằng số và :
\(\overrightarrow{p}=\left[\alpha.\overrightarrow{b}\overrightarrow{u}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{u}\right].\overrightarrow{u}+\left[\alpha.\overrightarrow{b}\overrightarrow{v}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{v}\right].\overrightarrow{v}\)
\(=\alpha.b\left(\overrightarrow{u}+t\overrightarrow{v}\right)+\left(1-\alpha\right).c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\)
\(=\alpha\overrightarrow{x}+\left(1-\alpha\right)\overrightarrow{y}\)
Trong đó \(\overrightarrow{x}=\overrightarrow{OX}=b\left(\overrightarrow{u}+t\overrightarrow{v}\right)\) và \(\overrightarrow{y}=\overrightarrow{OY}=c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\) là các vec tơ cố định
Suy ra P luôn nằm trên đường thẳng XY cố định khi \(\omega\) thay đổi

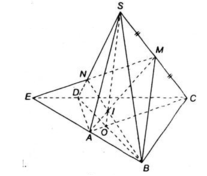
a) + Trong mp(ABCD), AB cắt CD tại E.
E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ Trong mp(SCD), EM cắt SD tại N.
Ta có:
N ∈ SD
N ∈ EM ⊂ mp(MAB)
Vậy N = SD ∩ mp(MAB)
b) Chứng minh SO, MA, BN đồng quy:
+ Trong mặt phẳng (SAC) : SO và AM cắt nhau.
+ trong mp(MAB) : MA và BN cắt nhau
+ trong mp(SBD) : SO và BN cắt nhau.
+ Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy.

Đáp án là C
Số tứ giác có 4 đỉnh là 4 điểm trong 13 điểm đã cho là C 8 2 . C 5 2 = 280
Mỗi tứ giác đó có hai đường chéo cắt nhau tại 1 điểm thuộc góc phần tư thứ nhất của hệ tọa độ Oxy
Vậy số giao điểm là 280.

TOÁN 6 :
a) \(\widehat{xOz}=\widehat{xOy}+\widehat{yOz}\)
\(100^O=50^O+\widehat{yOz}\)
\(\widehat{yOz}=100^o-50^o\)
\(\widehat{yOz}=50^o\)
b) Vì \(\widehat{xOy}=\widehat{yOz}=\dfrac{\widehat{xOz}}{2}=\dfrac{100^o}{2}=50^o\)
c) Vì Ox' là tia đối của Ox nên suy ra \(\widehat{xOx'}=180^o\)
\(\widehat{xOx'}=\widehat{xOz}+\widehat{zOx'}\)
\(180^o=100^o+\widehat{zOx'}\)
\(\widehat{zOx'}=180^o-100^o\)
\(\widehat{zOx'}=80^o\)


Giải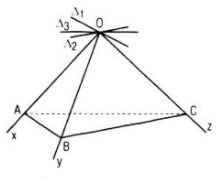
Giả sử Δ1, Δ2, Δ3 lần lượt là ba đường phân giác ngoài của các góc xOy, yOz, xOz. Nếu trên các tia Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC thì dễ thấy Δ1 // AB, Δ2 // BC, Δ3 // CA.
Vậy Δ1, Δ2, Δ3 đồng phẳng