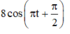Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

\(Z_L=100\Omega\)
\(Z_C=40\Omega\)
Theo giả thiết ta có:
\(R_1.R_2=(Z_L-Z_C)^2=60^2\)
\(R_1+R_2=\dfrac{U^2}{P}\)
\(\tan\varphi_1=\dfrac{60}{R_1}\)
\(\tan\varphi_2=\dfrac{60}{R_2}\)
Có: \(\varphi_1=2.\varphi_2\Rightarrow \tan \varphi_1=\tan 2\varphi_2=\dfrac{2\tan\varphi_2}{1-\tan^2\varphi_2}=\dfrac{60}{R_1}\)
\(\Rightarrow \dfrac{2\dfrac{60}{R_2}}{1-(\dfrac{60}{R_2})^2}=\dfrac{60}{R_1}\)
Biến đổi ta tìm đc \(R_2=60\sqrt 3\); \(R_1=20\sqrt 3\)
\(\Rightarrow P=\dfrac{U^2}{R_1+R_2}=60\sqrt 3(W)\)

Điểu chỉnh điện dung C của tụ thấy C = C1 và C = C2 thì có cùng giá trị hiệu dụng của tụ điện \(U_{C1} = U_{C2}\).
Khi đó để \(U_{Cmax}\) thì \(C=C_0 = \frac{C_1+C_2}{2}\)
Chọn đáp án.D.

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Áp dụng công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega^2} \Rightarrow\) \(8^2+\frac{12^2}{\omega^2} = 6^2+\frac{16^2}{\omega^2} \Rightarrow \omega = 2 \ (rad/s) \Rightarrow f = \frac{1}{\pi} \ Hz\)

 chọn A
chọn A
Đáp án C
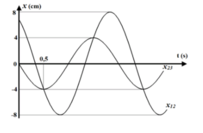
Từ đồ thị ta thấy
Tại t = 0,5 s thì x12 = -4 cm ®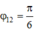
Vì A1 = 2A3 và j3 - j1 = p ® x1 = -2x3
Ta có: 2x23 = 2x2 + 2x3 =