Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

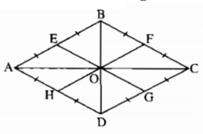
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).

a) Ta có : \(\hat{A}=90^o\) (góc nội tiếp chắn nửa đường tròn (O), đường kính BC).
\(\hat{E}=90^o\) (góc nội tiếp chắn nửa đường tròn (I), đường kính AH).
\(\hat{F}=90^o\) (góc nội tiếp chắn nửa đường tròn (I), đường kính AH).
Suy ra, AHEF là hình chữ nhật (dấu hiệu nhận biết) (điều phải chứng minh).
b) Ta có : \(\hat{HAC}+\hat{C}=90^o\) (hai góc phụ nhau) và \(\hat{ABC}+\hat{C}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{HAC}=\hat{ABC}\) (điều phải chứng minh).
Mặt khác : \(\hat{AEF}=\hat{AHF}\) (hai góc nội tiếp đường tròn (I) cùng chắn cung AF).
Và : \(\left\{{}\begin{matrix}\hat{AHF}+\hat{HAC}=90^o\\\hat{C}+\hat{HAC}=90^o\end{matrix}\right.\Rightarrow\hat{AHF}=\hat{C}\). Suy ra : \(\hat{AEF}=\hat{C}\).
Lại có : \(\hat{AEF}+\hat{BEF}=180^o\) (hai góc kề bù) \(\Rightarrow\hat{C}+\hat{BEF}=180^o\).
Mà trong tứ giác BEFC, hai góc trên lại đối nhau. Do đó, tứ giác BEFC nội tiếp được một đường tròn (điều phải chứng minh).


a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp