Question

[Phạm Thị Mai Chi]

cho a+b+c+d= 20 va ab+ac+ad+bc+bd+cd= 150. Tim a,b,c,d

Answer 1

[doraemon]

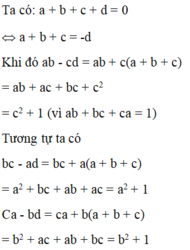
Vì a+b+c+d = 20 

=> \(\left(a+b+c+d\right)^2=400\)

<=> \(\left(a+b\right)^2+\left(c+d\right)^2+2\left(a+b\right)\left(c+d\right)=400\)

<=> \(a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd=400\)

<=> \(a^2+b^2+c^2+d^2+2\left(ab+ac+ad+bc+bd+cd\right)=400\)

<=> \(a^2+b^2+c^2+d^2+2.150=400\)

<=> \(a^2+b^2+c^2+d^2=100\)

Ta có: \(\left(a-b\right)^2\ge0\) (đúng với mọi a, b thuộc R)

<=> \(a^2+b^2\ge2ab\)

<=> \(\dfrac{a^2+b^2}{2}\ge ab\) (đúng với mọi a, b thuộc R)

Dấu = xảy ra <=> a - b = 0 <=> a = b

Áp dụng BĐT trên ta có: 

\(ab+ac+ad+bc+bd+cd\le\dfrac{a^2+b^2}{2}+\dfrac{a^2+c^2}{2}+\dfrac{a^2+d^2}{2}+\dfrac{b^2+c^2}{2}+\dfrac{b^2+d^2}{2}+\dfrac{c^2+d^2}{2}\)

                                                         \(=\dfrac{3a^2+3b^2+3c^2+3d^2}{2}\)

                                                         \(=\dfrac{3.100}{2}\)

                                                         \(=150\)

Vậy ta có \(ab+ac+ad+bc+bd+cd\le150\) (với mọi a, b, c, d thuộc R)

ab + ac + ad + bc + bd + cd = 150 <=> Dấu "=" xảy ra 

                                                                 <=> a = b = c = d = \(\dfrac{20}{4}\)= 5

Vậy a = b = c = d = 5