Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tam giác BMH đồng dạng với tam giác MCI => \(\frac{BM}{MC}=\frac{MH}{CI}=\frac{BH}{MI}\left(1\right)\)
từ (1) => MB.MC=\(\frac{MH}{CI}\).MC2=\(\frac{MH}{CI}\left(MI^2+IC^2\right)\)=MH.IC+\(\frac{MI}{IC}\cdot MI^2\)
hay MB.MC=IA.IC+\(\frac{BH}{MI}\cdot MI^2\)\(=IA\cdot IA+HB\cdot MI=IA\cdot IC+HB\cdot HA\)

1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)

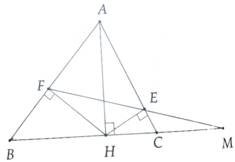
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC