Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D F E
Ta có DE//AC \(\Rightarrow\dfrac{AE}{AB}=\dfrac{CD}{BC}\) (Talet)
Ta có DF//AB \(\Rightarrow\dfrac{AF}{AC}=\dfrac{BD}{BC}\) (Talet)
\(\Rightarrow\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD}{BC}+\dfrac{BD}{BC}=\dfrac{BC}{BC}=1\left(dpcm\right)\)

Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
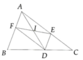

A B D C F E
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)
Xét `\triangle ABC` có:
`@ ED //// AC=>[AE]/[AB]=[DC]/[BC]`
`@DF //// AB=>[AF]/[AC]=[BD]/[BC]`
`=>[AE]/[AB]+[AF]/[AC]=[DC+BD]/[BC]=[BC]/[BC]=1` `(đpcm)`.