Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D C F E
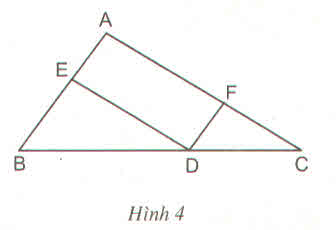
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)

Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \(\frac{AE}{AB}=\frac{CD}{CB}\)(định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \(\frac{AF}{AC}=\frac{BD}{BC}\)(định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
\(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)

DF//AB\(\Rightarrow\frac{AF}{AC}=\frac{BD}{BC}\)
Lại có DE//AC\(\Rightarrow\frac{BD}{BC}=\frac{BE}{AB}\)
Vậy \(\frac{AE}{AB}+\frac{AF}{AC}=\frac{AE}{AB}+\frac{EB}{AB}=\frac{AB}{AB}=1\)

bạn tự vẽ hình nha
Xét \(\Delta ABC\) , vì \(DE\) // \(AC\left(gt\right)\) , ta có :
\(\frac{AE}{AB}=\frac{CD}{CB}\left(1\right)\)
Mà \(DF\) // \(AB\left(gt\right)\) , ta có :
\(\frac{AF}{AC}=\frac{BD}{BC}\left(2\right)\)
Ta cộng hai vế (1) và (2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{CB}+\frac{BD}{BC}=\frac{CD+BD}{BC}=\frac{BC}{BC}=1\)

A B C D E F
Thấy đề sai sai á :)) Hóng cách làm vậy ....