Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C F D E
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE ( gt ) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu \(\Delta ABC\) vuông tại A thì AEDF là hình chữ nhật ( vì là hình bình hành có một góc vuông )
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông ( vì vừa là hình chữ nhật, vừa là hình thoi )

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

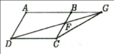
do E nằm trên AB mà FD song song với AB => FD song song với BE
=> FD/EB = CD/DB=CF/DF
=> tam giác BDE ~ DCF ( do có các cạnh tỉ lệ)
Ủa bạn ei có 2 câu hỏi mà