Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. xét ∆AMB và ∆AMC, có:
AB = AC (∆ABC cân tại A)
\(\widehat{BAM}=\widehat{CAM}\) (AM là tia phân giác)
AM là cạnh chung
=> ∆AMB = ∆AMC (c-g-c)
b. xét ∆ vuông EAM và ∆ vuông FAM, có:
\(\widehat{EAM}=\widehat{FAM}\) (AM là tia phân giác)
AM là cạnh chung
=> △EAM = △FAM (ch-gn)
=> AE = AF (2 cạnh tương ứng)
=> △AEF là △ cân tại A
c. vì △EAM = △FAM (câu b)
nên AE = AF, ME = MF (2 cạnh tương ứng)
=> AM là đường trung trực của đoạn thẳng EF
=> AM vuông góc với EF
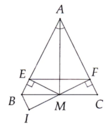
d. vì BI // AC => \(\widehat{AFM}=\widehat{BIM}=90^0\left(\text{so le trong}\right)\)
và \(\widehat{ACB}=\widehat{CBI}\) (so le trong)
xét △ vuông MEB và △ vuông MIB , có:
BM là cạnh chung
\(\widehat{MBE}=\widehat{MBI}\left(\text{cùng bằng }\widehat{ACB}\right)\)
=> △MEB = △MIB (ch - gn)
=> BE = BI (2 cạnh tương ứng)

A B C M I E F
a) _ Xét tam giác AME và tam giác AMF có :
E = F ( = 90 độ)
AM là cạnh huyền chung
A1=A2 ( AM là tia phân giác của BAC)
suy ra : tam giác AME = tam giác AMF ( CH-GN)
suy ra AE = AF ( 2 cạnh tương ứng)
suy ra tam giác AEF cân tại A
vẽ hình tạm nha
~ chúc bn học tốt~