NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VK
22 tháng 4 2017
a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
8 tháng 4 2021
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b
SG
1
SG
2
TP
15 tháng 3 2018
a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)
Mặt khác: 3b + 5 > 3b + 2 (2)
Từ (1) và (2) suy ra: 3a + 5 > 3b + 2
b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)
Mặt khác: 2 – 4a < 3 – 4a (2)
Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b
23 tháng 3 2023
a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)
Mặt khác: 3b + 5 > 3b + 2 (2)
Từ (1) và (2) suy ra: 3a + 5 > 3b + 2
b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)
Mặt khác: 2 – 4a < 3 – 4a (2)
Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b
21 tháng 9 2019
Áp dụng BĐT AM-GM cho 2 số dương, ta có:
\(\left(b+3c\right)+4\ge2\sqrt{4\left(b+3c\right)}=4\sqrt{b+3c}\\ \)
\(\Rightarrow\sqrt{b+3c}\le\frac{b+3c+4}{4}\)
\(\Rightarrow a\sqrt{b+3c}\le\frac{ab+3ac+4a}{4}\)
Tương tự ta có \(b\sqrt{c+3a}\le\frac{bc+3ab+4b}{4}\)
\(c\sqrt{a+3b}\le\frac{ac+3bc+4c}{4}\)
\(\Rightarrow a\sqrt{b+3c}+b\sqrt{c+3a}+c\sqrt{a+3b}\le\)\(\frac{4\left(ab+bc+ca\right)+4\left(a+b+c\right)}{4}\)\(=\frac{4\left(ab+bc+ac\right)+12}{4}\)
Ta có bổ đề:3(ab+bc=ca) \(\le\)(a+b+c)^2 => 3(ab+bc+ca) \(\le9\)=> \(\text{(ab+bc+ca)}\le3\)
=>\(a\sqrt{b+3c}+b\sqrt{c+3a}+c\sqrt{a+3b}\le\)\(\frac{4.3+12}{4}=6\left(đpcm\right)\)
Dấu "=" xảy ra <=>a=b=c=1
21 tháng 9 2019
Dùng điểm rơi a=b=1
Gọi M là biểu thức đầu bài ta có
\(M=\frac{3}{2}\sqrt{\left(3a+1\right).4}+\sqrt{\left(3b+1\right).4}\le\frac{3}{4}\left(3a+5\right)+\frac{1}{2}\left(3b+5\right)\)
\(=\frac{9a+6b}{4}+\frac{25}{4}=\frac{15}{4}+\frac{25}{4}=10\)
T
10 tháng 6 2019
#)Giải :
\(a^2+b^2\le1+ab\)
\(\Leftrightarrow a^2-ab+b^2\le1\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2\right)\le a+b\)
\(\Leftrightarrow a^3+b^3\le a+b\)
\(\Leftrightarrow\left(a^3+b^3\right)\left(a^3+b^3\right)\le\left(a+b\right)\left(a^5+b^5\right)\left(a^3+b^3=a^5+b^5\right)\)
\(\Leftrightarrow a^6+2a^3b^3+b^6\le a^6+ab^5+a^5b+b^6\)
\(\Leftrightarrow a^5b+ab^5\ge2a^3b^3\)
\(\Leftrightarrow a^5b+ab^5-2a^3b^3\ge0\)
\(\Leftrightarrow ab\left(a^4-2a^2b^2+b^4\right)\ge0\)
\(\Leftrightarrow ab\left(a^2-b^2\right)^2\ge0\)( luôn đúng \(\forall a;b>0\))
Vậy \(a^2+b^2\le1+ab\left(đpcm\right)\)
P/s : Bài này mk tham khảo trên mạng ( tại thấy rảnh nên chép hộ ^^ )
25 tháng 6 2019
17) \(\frac{10x^2-7x-5}{2x-3}\) là số nguyên khi 10x² - 7x - 5 \(⋮\) 2x - 3
Ta có: 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
\(\Rightarrow\) 10x² - 7x - 5 \(⋮\) 2x - 3 khi và chỉ khi 7 chia hết cho 2x-3
\(\Rightarrow\) 2x - 3 \(\in\) Ư(7) \(\Leftrightarrow\) 2x - 3 = \(\left\{-1;1;-7;7\right\}\)
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là \(\left\{-2;1;2;5\right\}\)
25 tháng 6 2019
23) Cm rằng
a) a2+b2−2ab ≥0
Ta có: a2+b2−2ab = a2−2ab+b2 = (a - b)2 ≥ 0 (đpcm)
b)\(\frac{a^2+b^2}{2}\) ≥ ab
Ta có: (a-b)2 ≥0 vs mọi a,b
\(\Leftrightarrow\) a2−2ab+b2 ≥0
\(\Leftrightarrow\) a2+b2 ≥ 2ab
\(\Leftrightarrow\) \(\frac{a^2+b^2}{2}\) ≥ ab (đpcm)
c) a(a+2)<(a+1)2
Ta có: a(a+2)= a2+2a
(a+1)2 = a2 + 2a + 1
\(\Rightarrow\) a(a+2)<(a+1)2 (đpcm)
d) m2+n2+2 ≥ 2(m+n)
Ta có: (m-n)2 \(\ge\) 0
\(\Leftrightarrow\) m2- 2mn+n2 \(\ge\) 0
\(\Leftrightarrow\) m2+n2 \(\ge\) 2mn
\(\Leftrightarrow\) m2+n2+2 \(\ge\) 2mn+2
\(\Leftrightarrow\) m2+n2+2 ≥ 2(m+n) (đpcm)
e) (a+b)(\(\frac{1}{a}+\frac{1}{b}\))≥4 (với a>0, b>0)
Ta có: (a - b)2 ≥ 0
\(\Leftrightarrow\) a2−2ab+b2 ≥ 0
\(\Leftrightarrow\) a2+2ab - 4ab+b2 ≥ 0
\(\Leftrightarrow\) (a + b)2 - 4ab≥ 0
\(\Leftrightarrow\) (a + b)2 ≥ 4ab
\(\Leftrightarrow\) \(\frac{\left(a+b\right)^2}{ab}\) ≥ 4
\(\Leftrightarrow\) (a+b) ( \(\frac{a+b}{ab}\) ) ≥ 4
\(\Leftrightarrow\) (a+b)(\(\frac{1}{a}+\frac{1}{b}\))≥4 (vs a,b > 0) (đpcm)
QT
2
17 tháng 3 2019
a, \(a^4+b^4-a^3b-ab^3=a^3\left(a-b\right)-b^3\left(a-b\right)\)
\(=\left(a-b\right)\left(a^3-b^3\right)=\left(a-b\right)^2\left(a^2+ab+b^2\right)\)
Mà \(\hept{\begin{cases}\left(a-b\right)^2\ge0\forall a;b\\a^2+ab+b^2=\left(a+\frac{1}{2}b\right)^2+\frac{3}{4}b^2\ge0\forall a;b\end{cases}}\)
\(\Rightarrow\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\)
\(\Rightarrow a^4+b^4-a^3b-ab^3\ge0\Leftrightarrow a^4+b^4\ge a^3b+ab^3\)
Dấu "=" xảy ra khi a = b
b, \(a^3-3a^2+4a+1=a\left(a^2-4a+4\right)+a^2+1=a\left(a-2\right)^2+a^2+1>0\left(\forall a>0\right)\)
c, \(a^4+b^2+2-4ab=\left(a^4-2a^2b^2+b^4\right)+\left(2a^2b^2-4ab+2\right)\)
\(=\left(a^2-b^2\right)^2+2\left(ab-1\right)^2\ge0\)
\(\Rightarrow a^4+b^4+2\ge4ab\)
Dấu "=" xảy ra khi \(\orbr{\begin{cases}a=b=1\\a=b=-1\end{cases}}\)
5 tháng 5 2017
a. Do \(a>0,\) \(b>0\) \(\Rightarrow a,b\) là số dương
Ta có:
* \(a< b\Leftrightarrow a^2< ab\) (nhân cả hai vế với a)
* \(a< b\Leftrightarrow ab< b^2\) (nhân cả hai vế với b)
b. Từ câu a theo tính chất bắc cầu suy ra:\(a^2< b^2\)
Ta có: \(a^2< b^2\Leftrightarrow a^3< ab^2\) (nhân cả hai vế với a)
mà ab2<b3 (a<b)
\(\Rightarrow a^3< b^3\)
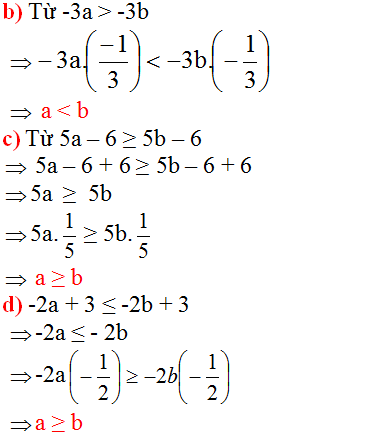
\(A< B\\ 3A< 3B\\ 3A+4< 3B+4\\\)
Mà \(3B+4< 3B+5\Rightarrow3A+4< 3B+5\)
\(A< B\\ -A>-B\\ -A+3>-B+3\)
Mà \(-A+6>-A+3\Rightarrow-A+6>-B+3\\ \Leftrightarrow6-A>3-B\)