Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?
Bài giải:
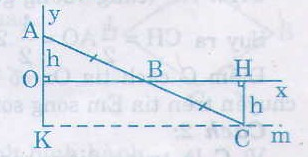
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
=
( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.

Từ \(\frac{a}{b}=\frac{c}{d}\)\(\Rightarrow\)\(\frac{a}{c}=\frac{b}{d}\)\(\Rightarrow\)\(\frac{5a}{5c}=\frac{3b}{3d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{5a}{5c}=\frac{3b}{3d}=\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)
Từ \(\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)\(\Rightarrow\)\(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)(đpcm)
_Chúc bạn học tốt_

a) Vì a/b=c/d nên a/c=b/d=>5a/5c=3b/3d=5a+3b/5c+3d=5a-3b/5a-3d(tính chất dãy tỉ số bằng nhau)(đpcm)
b)con b làm tương tự con a thôi

Đặt \(\frac{a}{b}=\frac{c}{d}=k=>a=bk,c=dk\)
=>\(\frac{5a+3b}{5a-3b}=\frac{5.bk+3b}{5.bk-3b}=\frac{5.bk-3b+3b+3b}{5.bk-3b}=1+\frac{6b}{\left(5k-3\right).b}=1+\frac{6}{5k-3}\)
\(\frac{5c+3d}{5c-3d}=\frac{5.dk+3d}{5.dk-3d}=\frac{5.dk-3d+3d+3d}{5.dk-3d}=1+\frac{6d}{\left(5k-3\right).d}=1+\frac{6}{5k-3}\)
=>\(\frac{5a+3b}{5a-3b}=1+\frac{6}{5k-3}=\frac{5c+3d}{5c-3d}\)
=>\(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)

a, a/b = c/d => a/c=b/d ( đây là tính chất tỉ lệ thức đó )
Khi đó lại áp dụng tính chất dãy tỉ số bằng nhau : a/c = b/d = a+b/c+d = a-b/c-d
Từ riêng cắp a+b/c+d=a-b/c-d vừa CM đc ở trên => a+b/a-b=c+d/c-d ( lại tính chất tỉ lệ thức nè )
Xong phần a nhé ^^
b, Phần a đã suy ra đc cặp a/c=b/d rồi đúng ko ?
Đặt a/c=b/d=k thì a=ck và b=dk
Khi đó 2a-3b/2a+3b=2ck-3dk/2ck+3dk= k.(2c-3d)/k.(2c+3d) ( Đặt k ra ngoài để nhóm)
= 2c-3d/2c+3d (Triệt tiêu k ở cả tử và mẫu)
Thế là xong nha ^^ thắc mắc gì nhắn hỏi riêng nhé :vv

\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ad=bc\)
Ta có:
Nếu:
\(\dfrac{2a+c}{2b+d}=\dfrac{a-c}{b-d}\Leftrightarrow\left(2a+c\right)\left(b-d\right)=\left(a-c\right)\left(2b+d\right)\)
\(\Leftrightarrow2a\left(b-d\right)+c\left(b-d\right)=a\left(2b+d\right)-c\left(2b+d\right)\)
\(\Leftrightarrow2ab-2ad+bc-cd=2ab+ad-2bc+cd\)
\(\Leftrightarrow ad=bc\)
\(\Leftrightarrow\dfrac{2a+c}{2b+d}=\dfrac{a-c}{b-d}\left(đpcm\right)\)

Đặt \(\frac{a}{b}=\frac{c}{d}=k\) (\(k\in N\)*)
\(\Rightarrow\begin{cases}a=bk\\c=dk\end{cases}\)\(\Rightarrow\frac{2bk-3b}{2bk+3b}=\frac{2dk-3d}{2dk+3d}\)
Xét vế trái \(\frac{2a-3b}{2a+3b}=\frac{2bk-3b}{2bk+3b}=\frac{b\left(2k-3\right)}{b\left(2k+3\right)}=\frac{2k-3}{2k+3}\left(1\right)\)
Xét vế phải \(\frac{2c-3d}{2c+3d}=\frac{2dk-3d}{2dk+3d}=\frac{d\left(2k-3\right)}{d\left(2k+3\right)}=\frac{2k-3}{2k+3}\left(2\right)\)
Từ (1) và (2) ta có Đpcm
Đặt ab=cd=kab=cd=k (k∈Nk∈N*)
⇒{a=bkc=dk⇒{a=bkc=dk⇒2bk−3b2bk+3b=2dk−3d2dk+3d⇒2bk−3b2bk+3b=2dk−3d2dk+3d
Xét vế trái 2a−3b2a+3b=2bk−3b2bk+3b=b(2k−3)b(2k+3)=2k−32k+3(1)2a−3b2a+3b=2bk−3b2bk+3b=b(2k−3)b(2k+3)=2k−32k+3(1)
Xét vế phải 2c−3d2c+3d=2dk−3d2dk+3d=d(2k−3)d(2k+3)=2k−32k+3(2)![]()
Vt lại đề nhé (khó nhìn)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\)
Chứng minh : \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=x\Rightarrow a=bx;c=dx\)
Lần lượt thay vào các vế, ta được :
\(\dfrac{5a+3b}{5a-3b}=\dfrac{5.b.x+3b}{5.b.x+3b}=\dfrac{b\left(5x+3\right)}{b\left(5x+3\right)}=\dfrac{5x+3}{5x+3}\left(1\right)\)
\(\dfrac{5c-3d}{5c-3d}=\dfrac{5.d.x-3d}{5.d.x-3d}=\dfrac{d\left(5x-3\right)}{d\left(5x-3\right)}=\dfrac{5x-3}{5x-3}\left(2\right)\)
Từ \(\left(1\right)và\left(2\right)\)
\(\Rightarrow\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\left(đpcm\right)\)