Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: vì M nằm trên trục Ox nên M(x;0)
\(\overrightarrow{MA}=\left(x_A-x_M;y_A-y_M\right)=\left(-3-x_M;2\right)\)
\(\overrightarrow{MB}=\left(x_B-x_M;y_B-y_M\right)=\left(4-x_M;3\right)\)
Ta có: ΔMAB vuông tại M
nên \(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\)
\(\Leftrightarrow\left(-3-x_M\right)\left(4-x_M\right)+6=0\)
\(\Leftrightarrow\left(x_M+3\right)\left(x_M-4\right)+6=0\)
\(\Leftrightarrow x_M^2-x_M-6=0\)
=>xM=3
Câu 1 đề thiếu, điểm C thỏa mãn điều gì nữa? (ví dụ G là trọng tâm tam giác?)
Câu 2:
Do B, C đều thuộc d nên tọa độ có dạng: \(B\left(2b-3;b\right);C\left(2c-3;c\right)\) với \(b\ne c\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2c-2;c-2\right)\\\overrightarrow{BC}=\left(2c-2b;c-b\right)\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{BC}=0\\AC=3BC\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(2c-2\right)\left(2c-2b\right)+\left(c-2\right)\left(c-b\right)=0\\\left(2c-2\right)^2+\left(c-2\right)^2=9\left(2c-2b\right)^2+9\left(c-b\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4c-4+c-2=0\\\left(2c-2\right)^2+\left(c-2\right)^2=45\left(c-b\right)^2\end{matrix}\right.\)
\(\Rightarrow...\)
Ta có d(I;d)=\(\sqrt{10}\ge2\) => d không cắt đường tròn Phương trình đường tròn x^2+(y-2)^2=4
Đặt M(a,b),N(c,d)
Vì M thuộc d,N thuộc đường tròn, A là trung điểm của MN
\(\hept{\begin{cases}a-3b-4=0\left(1\right)\\c^2+\left(d-2\right)^2=4\left(2\right)\\a+c=6,b+d=2\left(3\right)\end{cases}}\)
Từ (1) và (3)
=> 6-c-3(2-d)-4=0
=>c-3d=-4
Khi đó thế vào (2)
=>\(\left(3d-4\right)^2+\left(d-2\right)^2=4\)
=> \(10d^2-28d+16=0\)
=>\(\orbr{\begin{cases}d=2\\d=\frac{4}{5}\end{cases}}\)
+ d=2 => M(4;0),N(2;0)
+ d=4/5=> M(38/5;6/5),N(-8/5,4/5)
4.
Gọi H là chân đường cao kẻ từ C xuống đường thẳng d.
Ta có: \(CH=d\left(C;d\right)=\dfrac{\left|-3.2-4.5+4\right|}{\sqrt{3^2+4^2}}=\dfrac{22}{5}\)
Khi đó: \(S_{ABC}=\dfrac{1}{2}CH.AB=\dfrac{1}{2}.\dfrac{22}{5}.AB=15\Rightarrow AB=\dfrac{75}{11}\)
\(\Rightarrow IA=IB=\dfrac{75}{22}\)
Gọi \(A=\left(4m;3m+1\right)\) là điểm cần tìm.
Ta có: \(IA=\dfrac{75}{22}\Leftrightarrow\sqrt{\left(4m-2\right)^2+\left(3m-\dfrac{3}{2}\right)^2}=\dfrac{75}{22}\)
\(\Leftrightarrow\sqrt{25m^2-25m+\dfrac{25}{4}}=\dfrac{75}{22}\)
\(\Leftrightarrow\left|m-\dfrac{1}{2}\right|=\dfrac{15}{22}\)
\(\Leftrightarrow\left[{}\begin{matrix}m-\dfrac{1}{2}=\dfrac{15}{22}\\m-\dfrac{1}{2}=-\dfrac{15}{22}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{13}{11}\\m=-\dfrac{2}{11}\end{matrix}\right.\)
\(m=\dfrac{13}{11}\Rightarrow A=\left(\dfrac{52}{11};\dfrac{50}{11}\right)\Rightarrow B=\left(-\dfrac{8}{11};\dfrac{5}{11}\right)\)
Vậy \(A=\left(\dfrac{52}{11};\dfrac{50}{11}\right);B=\left(-\dfrac{8}{11};\dfrac{5}{11}\right)\)
1.
\(P=\left(m;m+1\right)\) là điểm cần tìm
\(\Rightarrow NP=\sqrt{\left(m-3\right)^2+m^2}=\sqrt{2m^2-6m+9}\)
Ta có: \(NM=NP\)
\(\Leftrightarrow\sqrt{\left(-1-3\right)^2+\left(2-1\right)^2}=\sqrt{2m^2-6m+9}\)
\(\Leftrightarrow m^2-3m-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}P=\left(4;5\right)\\P=\left(-1;0\right)\end{matrix}\right.\)
Vậy \(P=\left(4;5\right)\) hoặc \(P=\left(-1;0\right)\)
Đáp án D
Gọi hàm số cần tìm là y= ax + b
Đường thẳng d cắt trục Ox tại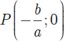 
và cắt Oy tại Q( 0 ;b) với a< 0; b> 0
Ta có tam giác OPQ cân tại O nên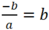 
hay b( a+1) =0
Suy ra b=0 (loại) hoặc a= -1
Ta có d qua M nên 2=a+ b nên b= 3
Vậy hàm số cần tìm là y= -x+ 3.
Chọn D.