Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn xem lại đề bài. Đề không đúng.
Đường thẳng d qua B thì B thuộc d
Đường thẳng d nằm trong (P) => d thuộc (P)
\(\Rightarrow\) B thuộc (P)
Nhưng thay tọa độ B vào d thì: \(2.2+2.1+3-7=2\ne0\) hoàn toàn không thỏa mãn
đề ghi như vậy, nhưng chắc là giáo viên cho đề sai, mình cũng lấy lạ
cảm ơn ạ

Đáp án B
Cách giải:
![]()
d : x - 2 1 = y - 1 - 2 = z - 1 2 có 1 VTCP v → =(1;-2;2) là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d ⇒ ∆ ⊂ ( α ) mặt phẳng qua A và vuông góc d mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng α
![]()
![]()
![]()
khi và chỉ khi đi qua hình chiếu H của B lên α
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của α có phương trình:
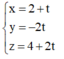
![]()
![]()
![]()
![]()
![]()
![]()

Chọn A
Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).
Suy ra (Q):2x+y+z-3=0.
Do Δ // (P) nên Δ ⊂ (Q)).
D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).
Gọi d là đường thẳng đi qua N và vuông góc (P), 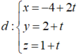
Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3 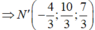
![]() cùng phương
cùng phương 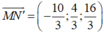
Do |a|, |b| nguyên tố cùng nhau nên chọn ![]()
Vậy |a| + |b| + |c| = 15.

Đáp án C
Phương pháp
Gọi H là hình chiếu của B trên mặt phẳng (Q) đi qua A và song song với (P). Khi đó
![]()
![]()
Cách giải
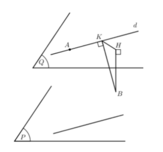
![]()
Gọi (Q) là mặt phẳng đi qua A và song song với (P) ta tìm được phương trình mặt phẳng (Q): (P): x-2y+2z-5=0, khi đó d ∈ (Q)
Gọi H là hình chiếu của B trên (Q) ta có
![]()
![]()
Phương trình đường thẳng d’ đi qua B và vuông góc với (Q) là
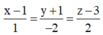
![]()
![]()
![]()
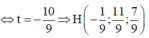
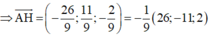
Vậy phương trình đường thẳng d cần tìm là d:
x + 3 26 = y 11 = z - 1 2

Chọn D
Đường thẳng d đi qua A nên d (B; d) ≤ BA, do đó khoảng cách từ B đến d lớn nhất khi ![]() , với là vectơ chỉ phương của d.
, với là vectơ chỉ phương của d.


Gọi (Q) là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là (x + 2) + 2(y + 1) - (z - 1) = 0 hay x + 2y - z + 5 = 0. Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử Δ là đường thẳng qua A và song song với (P), I là chân đường vuông góc kẻ từ B đến ∆ . Khi đó I ∈ (Q) và BH ≤ BI.
Do đó AH chính là đường phải tìm.
Gọi d là đường thẳng đi qua B và vuông góc với (Q).
Phương trình của d là:
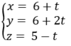
Để tìm giao điểm H = d ∩ (Q) ta thay phương trình của d vào phương trình của (Q), ta có:
6 + t + 2(6 + 2t) - (5 - t) + 5 = 0 ⇒ t = -3.
Do đó H = (3; 0; 8)
Phương trình đường thẳng AH là:
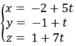
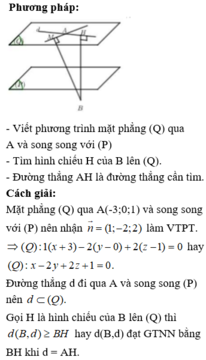
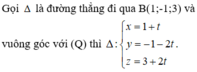
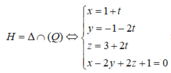
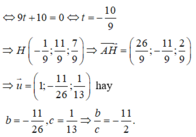




Gọi (Q) là mặt phẳng qua B và song song (P) \(\Rightarrow\) (Q) nhận \(\left(2;-2;1\right)\) là 1 vtpt
Phương trình (Q):
\(2\left(x-2\right)-2\left(y-1\right)+1\left(z-3\right)=0\)
\(\Leftrightarrow2x-2y+z-5=0\)
Gọi C là hình chiếu vuông góc của A lên (Q). Đường thẳng (d') qua A vuông góc (Q) nhận \(\left(2;-2;1\right)\) là 1 vtcp
Phương trình (d'): \(\left\{{}\begin{matrix}x=1+2t\\y=-2t\\z=-2+t\end{matrix}\right.\)
Tọa độ C thỏa mãn:
\(2\left(1+2t\right)-2\left(-2t\right)+\left(-2+t\right)-5=0\Rightarrow t=\frac{5}{9}\) \(\Rightarrow C\left(\frac{19}{9};-\frac{10}{9};-\frac{13}{9}\right)\)
\(\Rightarrow\overrightarrow{BC}=\left(\frac{1}{9};-\frac{19}{9};-\frac{40}{9}\right)=\frac{1}{9}\left(1;-19;-40\right)\)
\(\Rightarrow\left\{{}\begin{matrix}b=-19\\c=-40\end{matrix}\right.\)
Không có đáp án, đề ảo thật
Sure là làm đúng đó, chắc số liệu ko chính xác