Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương pháp
Gọi H là hình chiếu của B trên mặt phẳng (Q) đi qua A và song song với (P). Khi đó
Cách giải
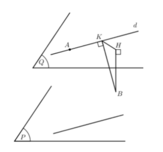
Gọi (Q) là mặt phẳng đi qua A và song song với (P) ta tìm được phương trình mặt phẳng (Q): (P): x-2y+2z-5=0, khi đó d ∈ (Q)
Gọi H là hình chiếu của B trên (Q) ta có
Phương trình đường thẳng d’ đi qua B và vuông góc với (Q) là
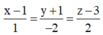
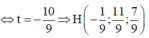
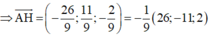
Vậy phương trình đường thẳng d cần tìm là d:
x + 3 26 = y 11 = z - 1 2
Chọn D
Xét hàm số:
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra 
. Chọn một vectơ chỉ phương của đường thẳng d là 
Vậy phương trình đường thẳng 
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)
Gọi (Q) là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là (x + 2) + 2(y + 1) - (z - 1) = 0 hay x + 2y - z + 5 = 0. Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử Δ là đường thẳng qua A và song song với (P), I là chân đường vuông góc kẻ từ B đến ∆ . Khi đó I ∈ (Q) và BH ≤ BI.
Do đó AH chính là đường phải tìm.
Gọi d là đường thẳng đi qua B và vuông góc với (Q).
Phương trình của d là:
Để tìm giao điểm H = d ∩ (Q) ta thay phương trình của d vào phương trình của (Q), ta có:
6 + t + 2(6 + 2t) - (5 - t) + 5 = 0 ⇒ t = -3.
Do đó H = (3; 0; 8)
Phương trình đường thẳng AH là:
Chọn D
Đường thẳng d đi qua A nên d (B; d) ≤ BA, do đó khoảng cách từ B đến d lớn nhất khi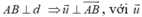
, với là vectơ chỉ phương của d.