Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 2
tổng vật liệu cần chở là 4,5.20= 90 (tạ)
=> nếu mỗi xe chở 6 tạ thì cần chở 15 chuyến

Lời giải:
Theo như đề thì hàm lợi nhuận (y) và sản lượng (x) sẽ có dạng này:
Hàm lợi nhuận có dạng pt như sau:
$y=ax^2+bx+c$
Sản lượng bằng $0$ thì lợi nhuận đương nhiên bằng $0$
$\Rightarrow c=0$
ĐTHS đổi dấu tại $x=10$, tức là $x=10$ là điểm cực trị
$\Rightarrow \frac{b}{-2a}=10\Leftrightarrow b=-20a$
$y=ax^2-20ax$. Thay $x=5; y=170$ thì $a=-\frac{34}{15}$
Vậy hàm lợi nhuận là: $y=\frac{-34}{15}x^2+\frac{136}{3}x$
Tại $x=12$ thì $y=217,6$
Hàm lợi nhuận giảm với tốc độ là \(|y'(12).\frac{12}{217,6}|=0,5\) (%)
Vậy tại mức sản phẩm 12, khi mức sản phẩm tăng 1% thì lợi nhuận giảm 0,5 %.

\(y'=-x^2+2\left(m-3\right)x+m+4\)
a.
Hàm nghịch biến trên khoảng đã cho khi và chỉ khi: với mọi \(x\in\left(-1;3\right)\) ta có:
\(f\left(x\right)=-x^2+2\left(m-3\right)x+m+4\le0\)
\(\Delta'=\left(m-3\right)^2+m+4=m^2-5m+13>0\) ; \(\forall m\)
Bài toán thỏa mãn khi:
\(\left[{}\begin{matrix}3\le x_1< x_2\\x_1< x_2\le-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}f\left(3\right)\le0\\\dfrac{x_1+x_2}{2}>3\end{matrix}\right.\\\left\{{}\begin{matrix}f\left(-1\right)\le0\\\dfrac{x_1+x_2}{2}< -1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}7m-23\le0\\m-3>3\end{matrix}\right.\\\left\{{}\begin{matrix}-m+9\le0\\m-3< -1\end{matrix}\right.\end{matrix}\right.\)
Không tồn tại m thỏa mãn
b.
Hàm nghịch biến trên khoảng đã cho khi và chỉ khi:
\(\forall x\in\left(2;4\right)\) ta có:
\(-x^2+2\left(m-3\right)x+m+4\le0\)
\(\Leftrightarrow x^2+6x-4\ge m\left(2x+1\right)\)
\(\Leftrightarrow m\le\dfrac{x^2+6x-4}{2x+1}\)
\(\Leftrightarrow m\le\min\limits_{\left[2;4\right]}\dfrac{x^2+6x-4}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+6x-4}{2x+1}\) trên \(\left[2;4\right]\)
\(f'\left(x\right)=\dfrac{x^2+x+7}{2\left(2x+1\right)^2}>0\) ; \(\forall x\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow m\le f\left(2\right)=\dfrac{12}{5}\)

Đáp án A.
Hàm số có y = x4 – x + 2 không là hàm số chẵn nên mệnh đề I sai.
Mệnh đề II, III, IV đúng

Chọn A
Ta có: f ' x = 3 a x 2 + 2 b x + c
có ∆ ' f ' x = b 2 - 3 a c .
Hàm số f x nghịch biến trên ℝ khi và chỉ khi
3 a < 0 ∆ ' f ' x ≤ 0
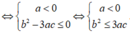

O A B C D B' A' D' C' M K O a a
a. Từ giả thiết ta có :
\(C\left(a;a;0\right);C'\left(a;a;b\right);D'\left(0;a;b\right);B'\left(a;0;b\right)\)
Vì M là trung điểm của CC' nên \(M=\left(a;a;\frac{b}{2}\right)\)
Ta có :
\(\overrightarrow{BD}=\left(-a;a;0\right)\)
\(\overrightarrow{BA}=\left(-a;0;b\right)\)
\(\overrightarrow{BM}=\left(0;a;\frac{b}{2}\right)\)
Vì thế \(\left[\overrightarrow{BD};\overrightarrow{BA'}\right]=\left(\left|\begin{matrix}a&0\\0&b\end{matrix}\right|;\left|\begin{matrix}0&-a\\b&-a\end{matrix}\right|;\left|\begin{matrix}-a&a\\-a&0\end{matrix}\right|\right)\)
\(=\left(ab,ab,a^2\right)\)
Vậy \(V_{BDa'M}=\frac{1}{6}\left|\left[\overrightarrow{BD};\overrightarrow{BA'}\right].\overrightarrow{BM}\right|=\frac{1}{6}\left|a^2b+\frac{a^2b}{2}\right|=\frac{a^2b}{4}\)
b. Gọi K là trung điểm của BD. Do \(A'B=A'D\Rightarrow A'K\perp BD\)
Lại có \(MB=MD\Rightarrow MK\perp BD\)
Vậy \(\widehat{A'KM}=90^0\)
\(\Leftrightarrow\overrightarrow{A'K}.\overrightarrow{MK}=0\)
Ta có :
\(K=\left(\frac{a}{2};\frac{a}{2};0\right)\) do đó :
\(\overrightarrow{A'K}=\left(\frac{a}{2};\frac{a}{2};-b\right)\)
\(\overrightarrow{MK}=\left(-\frac{a}{2};\frac{-a}{2};\frac{-b}{2}\right)\)
Vậy \(\left(1\right)\Leftrightarrow-\frac{a^2}{4}-\frac{a^2}{4}+\frac{b^2}{2}=0\)
\(\Leftrightarrow b^2=a^2\)
\(\Leftrightarrow\frac{a}{b}=1\)
Do (a>0,b>0) vì thế \(\left(A'BD\right)\perp\left(MBD\right)\Leftrightarrow\frac{a}{b}=1\)

\(\overrightarrow{AB}=\left(8;0;-2\right)=2\left(4;0;-1\right)\)
Phương trình AB có dạng: \(\left\{{}\begin{matrix}x=5+4t\\y=2\\z=2-t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(5+4t+2-3\left(2-t\right)+4=0\) \(\Rightarrow t=-\dfrac{5}{7}\)
\(\Rightarrow M\left(\dfrac{15}{7};2;\dfrac{19}{7}\right)\) \(\Rightarrow\left\{{}\begin{matrix}MA=\dfrac{9\sqrt{17}}{7}\\MB=\dfrac{5\sqrt{17}}{7}\end{matrix}\right.\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{9}{5}\)
Giải:
Ví số a và b tỉ lệ nghịch với nhau
\(\Rightarrow4a=5b\) hay \(\frac{a}{5}=\frac{b}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{4}=\frac{b-a}{4-5}=\frac{27}{-1}=-27\)
+) \(\frac{a}{5}=-27\Rightarrow a=-135\)
+) \(\frac{b}{4}=-27\Rightarrow b=-108\)
Vậy cặp số \(\left(a;b\right)\) là \(\left(-135;-108\right)\)