Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có ![]()
Xét hàm ![]()
Tập xác định D = (0; 10).
![]()
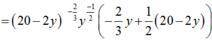
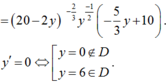
Nhận xét: ![]() nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức ![]()
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy ![]()

Giá của x sản phẩn là:
x ( 120 -x ) = - x2 +120x
Lợi nhuận còn lại:
\(-x^2+120x-C\left(x\right)=-x^2+120x-x^2-5x-300=-2x^2+115x-300\)

Ta có x ∈ (0; 60000)
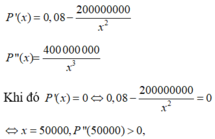
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C

Ta có x ∈ (0; 250) ,P’(x) = -16x+3200.
Khi đó P’(x)=0 ⇔ -16x + 3200 = 0 ⇔ x = 200 (loại).
P(0)= - 8000; P(250) = 292 000
Do đó lợi nhuận tối đa họ thu được là P(250)=292000
Chọn C

Gọi A là biến cố "sản phẩm chọn được từ lô 2 là loại A"
\(B_1\) là biến cố "viên bi được lấy ra là viên của hộp 1" \(\Rightarrow P\left(B_1\right)=\dfrac{C_5^1}{C_{20}^1}=\dfrac{1}{4}\)
\(B_2\) là biến cố "viên bi được lấy ra là viên bi của hộp 2" \(\Rightarrow P\left(B_2\right)=\dfrac{C_{15}^1}{C_{20}^1}=\dfrac{3}{4}\)
\(P\left(A|B_1\right)=\dfrac{C_3^1}{C_7^1}=\dfrac{3}{7}\)
\(P\left(A|B_2\right)=\dfrac{C_9^1}{C_{15}^1}=\dfrac{3}{5}\)
Xác suất:
\(P\left(A\right)=\dfrac{1}{4}.\dfrac{3}{7}+\dfrac{3}{4}.\dfrac{3}{5}=\dfrac{39}{70}\)
Áp dụng lợi nhuận = 170 thì không ra được ạ
Lời giải:
Theo như đề thì hàm lợi nhuận (y) và sản lượng (x) sẽ có dạng này:
Hàm lợi nhuận có dạng pt như sau:
$y=ax^2+bx+c$
Sản lượng bằng $0$ thì lợi nhuận đương nhiên bằng $0$
$\Rightarrow c=0$
ĐTHS đổi dấu tại $x=10$, tức là $x=10$ là điểm cực trị
$\Rightarrow \frac{b}{-2a}=10\Leftrightarrow b=-20a$
$y=ax^2-20ax$. Thay $x=5; y=170$ thì $a=-\frac{34}{15}$
Vậy hàm lợi nhuận là: $y=\frac{-34}{15}x^2+\frac{136}{3}x$
Tại $x=12$ thì $y=217,6$
Hàm lợi nhuận giảm với tốc độ là \(|y'(12).\frac{12}{217,6}|=0,5\) (%)
Vậy tại mức sản phẩm 12, khi mức sản phẩm tăng 1% thì lợi nhuận giảm 0,5 %.