
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để giải bài toán này, ta sẽ sử dụng các công thức và quy tắc trong lượng giác để tính toán.
Trước hết, ta có: sin(α+β) = sinα.cosβ + cosα.sinβ cos(α+β) = cosα.cosβ - sinα.sinβ
Đề bài cho α+β = 1313 và tanα = -2tanβ. Ta có thể suy ra các thông tin sau: tanα = -2tanβ => sinα/cosα = -2sinβ/cosβ => sinα.cosβ = -2sinβ.cosα
Bài toán yêu cầu tính A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12)
Để tính A, ta sẽ thay các giá trị đã biết vào công thức trên:
A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12))
Tuy nhiên, để tính giá trị chính xác của A, cần biết thêm giá trị cụ thể của α và β. Trong câu hỏi của bạn, không có thông tin về α và β, do đó không thể tính toán giá trị của A.

1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)

a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)

a) Đúng.
(α) ⊥ (β) ⇒ ∃ đường thẳng d ⊂ (β) và d ⊥ (α ).
Mà (α ) // (γ)
⇒ d ⊥ (γ)
⇒ (β) ⊥ (γ).
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
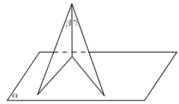

Đáp án D
Ta có
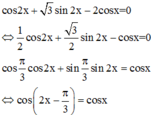
Do đó để phương trình ![]() tương đương với phương trình
tương đương với phương trình
![]()

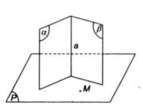
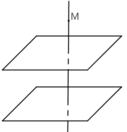

Vậy (MHK) chính là mặt phẳng đi qua M và vuông góc với (α) và (β).
Kết quả: Mặt phẳng (P) cần dựng (tức mp(MHK)) là mặt phẳng đi qua M và vuông góc với Δ.
Vì qua một điểm chỉ có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước nên (P) là duy nhất.
Nếu (α) // (β) thì qua M ta chỉ có thể vẽ một đường thẳng Δ vuông góc với (α) và (β). Bất kì mặt phẳng (P) nào chứa Δ cũng đều vuông góc với (α), (β). Trường hợp này, qua M có vô số mặt phẳng vuông góc với (α), (β).
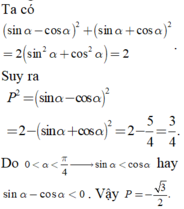
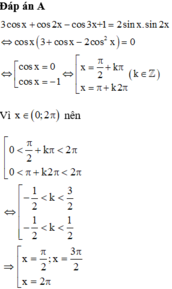
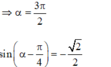
Đáp án B