Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có y ' = x 2 + 1 + x + 1 x x 2 + 1 x 2 + 1 = 0 ⇔ x 2 + 1 - x 2 - x = 0 ⇔ x = 1
Hàm số trên xác định và liên tục trên [-1;2]
Ta có y - 1 = 0 ; y 1 = 2 ; y 2 = 3 5
Do đó T = [ - 1 ; 2 ] ⇒ a 2 + b 2 = 2

Đáp án B
Hàm số đã cho xác định khi và chỉ khi x + 3 > 0 5 − x ≥ 0 ⇔ − 3 < x ≤ 5 . Vậy D = − 3 ; 5 ⊂ − 3 ; 5

Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Đáp án D
Câu C đúng theo điều kiện cần của cực trị.
Câu A, B đúng theo điều kiện đủ của cực trị. Câu D sai theo điều kiện đủ cho cực trị tồn tại
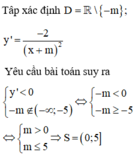

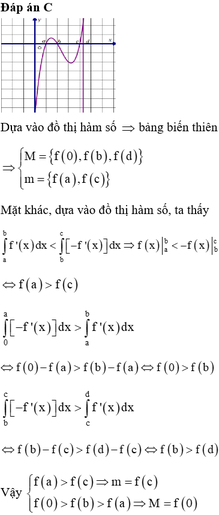
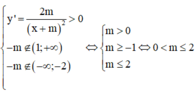

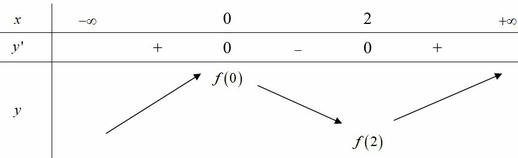




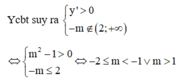
Đáp án A.
Hàm số y = a x có tập giá trị là 0 ; + ∞ ; tập giá trị của hàm số y = log a x là khoảng − ∞ ; + ∞ .