K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

LH
7 tháng 4 2017
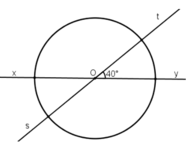
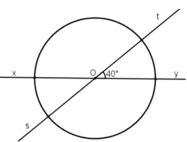
Ta có :
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)

9 tháng 6 2016
Bài này hôm qua mình giải rồi. bạn xem bài những bài giải lớp 9 ngày hôm qua sẽ có nhé

20 tháng 4 2018
Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng

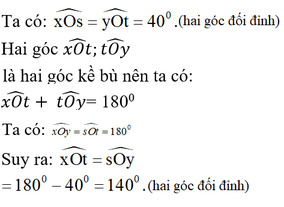
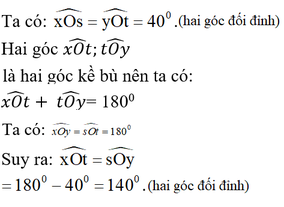
Ta chọn điểm O bất kì nằm trong mặt phẳng chứa 5 đường thẳng ấy. Qua O ta dựng các đường thẳng song song với các đường thẳng đã cho , khi đó có 10 góc đôi một đối đỉnh qua O . Vậy sẽ có ít nhất một góc không vượt quá \(\frac{180^o}{5}=36^o\)
'
'
'
'
'
'