Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
· Bổ đề: Trong mặt phẳng cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm A 1 , A 2 , . . . , A 10 và trên tia Oy lấy 10 điểm B 1 , B 2 , . . . . , B 10 thỏa mãn O A 1 = A 1 A 2 = . . . = A 9 A 10 = O B 1 = B 1 B 2 = . . . . = B 9 B 10 = 1 (đvd).
Tìm số tam giác có 2 đỉnh nằm trong 10 điểm 
1 đỉnh nằm trong 10 điểm
B
1
,
B
2
,
.
.
.
.
,
B
10
sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
Giải: Gọi 
là 3 đỉnh của tam giác thỏa yêu cầu bài toán với 
Ta có 
Do đường tròn luôn cắt Ox tại 
phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại
B
p
ta có phương tích
Do 
nên dễ thấy 
hay nói cách khác bộ ba (m,n,p) 
Vậy có 4 tam giác thỏa mãn yêu cầu bổ đề.
· Bài toán: Không gian mẫu 
Gọi A là biến cố chọn được tam giác có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy. Theo bổ đề ta chọn được 4 tam giác có 2 đỉnh thuộc tia Ox, 1 đỉnh thuộc tia Oy; tương tự có 4 tam giác có 1 đỉnh thuộc tia Oy, đỉnh thuộc tia . Suy ra, n(A) = 8
Xác suất biến cố A là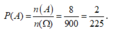 
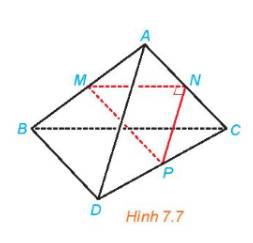
+) Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, AC
\( \Rightarrow \) MN là đường trung bình của tam giác ABC
\( \Rightarrow \) MN // BC
Mà NP \( \bot \) MN nên NP \( \bot \) BC
Xét tam giác ADC có
N, P lần lượt là trung điểm của AC, CD
\( \Rightarrow \) PN là đường trung bình của tam giác ADC
\( \Rightarrow \) PN // AD
Mà NP \( \bot \) BC nên AD \( \bot \) BC
+) BC // MN mà \(MN \subset \left( {MNP} \right) \Rightarrow BC//\left( {MNP} \right)\)
PN // AD mà \(PN \subset \left( {MNP} \right) \Rightarrow AD//\left( {MNP} \right)\)
Vậy AD và BC chéo nhau.
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
=>BC vuông góc NP
Xét ΔCAD có CN/CA=CP/CD
nên NP//AD
mà BC vuông góc NP
nên BC vuông góc AD
PN//AD
=>AD//(MNP)
BC//NP
=>BC//(MNP)
=>AD và BC chéo nhau
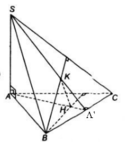
\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)
a: Sửa đề; BC vuông góc SB
BC vuông góc AB
BC vuông góc SA
=>BC vuôg góc (SAB)
=>CB vuông góc SB
c: (SO;(SCD))=(SO;SK)=góc KSO(OK vuông góc DC tại K)
\(AO=\dfrac{AC}{2}=1.5a\)
\(SA=\sqrt{SC^2-AC^2}=\sqrt{\left(5a\right)^2-\left(3a\right)^2}=4a\)
\(SO=\sqrt{SA^2+AO^2}=\dfrac{a\sqrt{73}}{2}\)
\(AD=BC=\sqrt{\left(3a\right)^2-a^2}=2a\sqrt{2}\)
Xét ΔACD có
O là trung điểm của AC
OK//AD
=>K là trung điểm của CD
=>DK=CK=a/2
\(AK=\sqrt{\left(2a\sqrt{2}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{33}}{2}\)
\(SK=\sqrt{SA^2+AK^2}=\sqrt{\left(4a\right)^2+\dfrac{33}{4}a^2}=\dfrac{a\sqrt{97}}{2}\)
OK=AD/2=a căn 2
\(SO=\dfrac{a\sqrt{73}}{2}\)
\(cosKSO=\dfrac{SK^2+SO^2-OK^2}{2\cdot SK\cdot SO}\simeq0.96\)
=>góc KSO=16 độ
Câu c bn ch c/m đc OK vuông góc vs mp (SCD)
Thì sao xác định đc góc cần tìm là OSK