OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
M
Mynnie
27 tháng 7 2018 - olm
Giải giúp mình các bài này với ạ!1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB = ACa. CM : Tam giác OAB = tam giác OACb. CM : AC là tiếp tuyến của đường tròn tâm Oc. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) = 5cm, BC = 8cm2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không...
Đọc tiếp

Giải giúp mình các bài này với ạ!

1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB = AC
a. CM : Tam giác OAB = tam giác OAC
b. CM : AC là tiếp tuyến của đường tròn tâm O
c. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) = 5cm, BC = 8cm

2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không thẳng hàng). Tiếp tuyến của O tại A cắt tia phân giác của góc AOB tại C.
a. So sánh tam giác OAC và tam giác OBC.
b. CM : BC là tiếp tuyến của đường tròn tâm O

3) Cho đường tròn tâm O, bán kính R. Lấy điểm A cách O một khoảng = 2R. Từ A vẽ 2 tiếp tuyến AB, AC (B,C là tiếp điểm). OA cắt đường tròn tâm O tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a. CM : OK // AB
b. CM : tam giác OAK là tam giác cân
c. CM : KI là tiếp tuyến của đường tròn tâm O.
#Toán lớp 9
0
SP
shoppe pi pi pi pi
21 tháng 11 2019 - olm

Cho hai đường tròn (O;R) và (O';R') tiếp xúc ngoài tại A (R> R').Vẽ các đường kính AOB ,AO'C .Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC .
a/ Chứng minh rằng tứ giác BDCE  là hình thoi 
b/ Gọi I là giao điểm của EC và đường tòn (O').Chứng minh rằng 3 điểm D,A,I thẳng hàng 
c/Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
#Toán lớp 9
0
SG
Sách Giáo Khoa
27 tháng 4 2017

Cho hai đườngtròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.

a) Chứng minh rằng tứ giác DBCE là hình thoi

b) Gọi I là giao điểm của EC và đường tròn (O'). Chứng minh rằng ba điểm D, A, I thẳng hàng

c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
#Toán lớp 9
1
NT
Nguyen Thuy Hoa
23 tháng 6 2017

Đường tròn

Đúng(0)
V
Voduytan
7 tháng 3 2018 - olm
Câu hỏi hay
Cho đường tròn (O;R), đường kính AC, trên bán kính OA lấy điểm B tùy ý (B khác O và A). Vẽ đường tròn tâm N đường kính AB. Gọi M là trung điểm của BC. Qua M vẽ dây DE vuông góc với BC, AD cắt (N) tại I.a. CM tứ giác BMDI nội tiếpb. 3 điểm I, B, E thẳng hàngc. MI là tiếp tuyến của (N)d. đường tròn tâm D bán kính DM cắt (O) tại P và Q. CM PQ qua trung điểm của MD.Giúp tớ câu d...
Đọc tiếp

Cho đường tròn (O;R), đường kính AC, trên bán kính OA lấy điểm B tùy ý (B khác O và A). Vẽ đường tròn tâm N đường kính AB. Gọi M là trung điểm của BC. Qua M vẽ dây DE vuông góc với BC, AD cắt (N) tại I.

a. CM tứ giác BMDI nội tiếp

b. 3 điểm I, B, E thẳng hàng

c. MI là tiếp tuyến của (N)

d. đường tròn tâm D bán kính DM cắt (O) tại P và Q. CM PQ qua trung điểm của MD.

Giúp tớ câu d với
#Toán lớp 9
4
M
miharachiharu
8 tháng 3 2018
là câu a
Đúng(0)
A
Anh2Kar六
8 tháng 3 2018

Ta có: ^BIC = 90o (do chắn đk BC) 
mà ^OMD = 90o (do DE _|_AB) 
=> tg BDMI nội tiếp 

Đúng(0)
XT
Xuân Trà
7 tháng 9 2016
Bài 1: Cho đường tròn tâm O, đường kính AB. Lấy C thuộc đường tròn tâm O. Kẻ tiếp tuyến tại A của đường tròn tâm O cắt BC tại D. Gọi M là trung điểm của AD.a) CM: MC là tiếp tuyến của đường tròn tâm Ob) CM: MO vuông góc với AC tại trung điểm I của ACBài 2: Từ điểm P nằm ngoài đường tròn tâm O bán kính R. Vẽ 2 tiếp tuyến PA, PB (A, B là các tiếp điểm). Gọi H là chân đường vuông góc...
Đọc tiếp

Bài 1: Cho đường tròn tâm O, đường kính AB. Lấy C thuộc đường tròn tâm O. Kẻ tiếp tuyến tại A của đường tròn tâm O cắt BC tại D. Gọi M là trung điểm của AD.

a) CM: MC là tiếp tuyến của đường tròn tâm O

b) CM: MO vuông góc với AC tại trung điểm I của AC
Bài 2: Từ điểm P nằm ngoài đường tròn tâm O bán kính R. Vẽ 2 tiếp tuyến PA, PB (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A đến đường kính BC. Chứng minh rằng PC giao AH tại trung điểm I của AH
#Toán lớp 9
0
PD
Phạm Duy Hùng
10 tháng 1 2021
cho đường tròn tâm O bán kính R và điểm A nằm ngoài đường tròn từ A kẻ tiếp tuyến AE với đường tròn tâm (O),C,E là các tiếp điểm vẽ dây EH vuông góc OA tại M a)biết R bằng ,OM bằng 3 cm tính EH b)CM AH là tiếp tuyến của đường tròn tâm O c)đường thẳng qua O vuông góc OA cắt AH tại B vẽ tiếp tuyến BF với đường tròn tâm O (F là tiếp điểm) CM EOF thằng hàng và...
Đọc tiếp

cho đường tròn tâm O bán kính R và điểm A nằm ngoài đường tròn từ A kẻ tiếp tuyến AE với đường tròn tâm (O),C,E là các tiếp điểm vẽ dây EH vuông góc OA tại M a)biết R bằng ,OM bằng 3 cm tính EH b)CM AH là tiếp tuyến của đường tròn tâm O c)đường thẳng qua O vuông góc OA cắt AH tại B vẽ tiếp tuyến BF với đường tròn tâm O (F là tiếp điểm) CM EOF thằng hàng và BF.AE=R^2
#Toán lớp 9
0
QV
Quang vo cong
2 tháng 6 2016 - olm
Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.a/ CM CIME nội tiếp.b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.c/ CM IE là tiếp tuyến của đường tròn tâm J.d/ Đường tròn tâm M bán kính MI cắt...
Đọc tiếp

Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.
a/ CM CIME nội tiếp.
b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.
c/ CM IE là tiếp tuyến của đường tròn tâm J.
d/ Đường tròn tâm M bán kính MI cắt đường tròn tâm O tại P và Q, Gọi H là giao điểm của PQ và MN. Tính tỉ số HM/HN
#Toán lớp 9
0
PT
Pham Trong Bach
19 tháng 12 2018

Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Gọi I là giao điểm của EC và đường tròn (O’). Chứng minh rằng ba điểm D, A, I thẳng hàng
#Toán lớp 9
1
CM
Cao Minh Tâm
19 tháng 12 2018

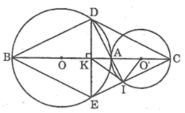
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D

Suy ra: AD ⊥ BD

Tứ giác BDCE là hình thoi nên EC // BD

Suy ra: EC ⊥ AD     (1)

Tam giác AIC nội tiếp trong đường tròn (O’) có AC là đường kính nên vuông tại I

Suy ra: AI ⊥ CE     (2)

Từ (1) và (2) suy ra AD trùng với AI

Vậy D, A, I thẳng hàng.

Đúng(0)
T
tranvandat
2 tháng 3 2019 - olm
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Vẽ tiếp tuyến AM,AN với đường tròn tâm O . Đường thẳng chứa đường kính của đường tròn song song với MN cắt AM tại B và cắt AN tại C .a, Gọi I là giao điểm của AC và đường tròn tâm O. CMR: I là tâm đường tròn nội tiếp tam giác AMNb,CM tứ giác MNCB là hình thang cânc, CM: MA.MB=R2d, Lấy D thuộc cung nhỏ MN vẽ tiếp tuyến...
Đọc tiếp

Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Vẽ tiếp tuyến AM,AN với đường tròn tâm O . Đường thẳng chứa đường kính của đường tròn song song với MN cắt AM tại B và cắt AN tại C .

a, Gọi I là giao điểm của AC và đường tròn tâm O. CMR: I là tâm đường tròn nội tiếp tam giác AMN

b,CM tứ giác MNCB là hình thang cân

c, CM: MA.MB=R2

d, Lấy D thuộc cung nhỏ MN vẽ tiếp tuyến đường tròn tâm O qua D cắt AM,AN lần lượt tại P và Q . CM: BP.CQ=BC2/4
#Toán lớp 9
2
CT
Cố Tử Thần
2 tháng 3 2019

bn làm đc câu nào rồi

Đúng(0)
T
tranvandat
4 tháng 3 2019

làm được xong ý c rồi còn ý d nữa bn làm dc ko giúp mik vs

Đúng(0)
KQ
KHANH QUYNH MAI PHAM
25 tháng 8 2019 - olm
Cho đường tròn tâm O, bán kính R và một điểm A sao cho OA=2R. VẼ các tiếp tuyến AB,AC ( B,C) là các tiếp điểm. Đường thẳng OA cắt BC tại H,  cắt cung nhỏ BC và cung lớn BC lần lượt tại I,Ka/ CM OA vuông góc với BC, HI=OA=R bình phươngb/ CM tam gaics ABC đều, tứ giác ABKC là hình thoic/ CHứng tỏ I là tâm đường tròn nội tiếp tam giác ABC. Tính theo R bán kính của đường tròn này. d/ Vẽ cát tueyens...
Đọc tiếp

Cho đường tròn tâm O, bán kính R và một điểm A sao cho OA=2R. VẼ các tiếp tuyến AB,AC ( B,C) là các tiếp điểm. Đường thẳng OA cắt BC tại H,  cắt cung nhỏ BC và cung lớn BC lần lượt tại I,K

a/ CM OA vuông góc với BC, HI=OA=R bình phương

b/ CM tam gaics ABC đều, tứ giác ABKC là hình thoi

c/ CHứng tỏ I là tâm đường tròn nội tiếp tam giác ABC. Tính theo R bán kính của đường tròn này. 

d/ Vẽ cát tueyens bất kì AMN của đường tròn tâm O. Gọi E là tủng điểm MN. CHứng tỏ 5 điểm O,E,A,B,C cùng thuộc một đường tròn
#Toán lớp 9
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP