Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x A y C t B x y
Câu a ta có :
At > yy (gt)
mà xx /yy (gt)
At yy ( hệ quả tiền đề Ô =lít)
câu b:
Vì AT tia phân giác xAb
=> xAt = =BaT =40 độ
Vậy :
bCE>BEC
~Study well~

Ta có: \(\widehat{xAB}=\widehat{ABy'}\)\(\left(xx'//yy',soletrong\right)\)(1)
Mà A1 là phân giác của \(\widehat{xAB}\)nên \(\widehat{xA_1}=\widehat{_1AB}=\frac{\widehat{xAB}}{2}\)(2)
Chứng minh tương tự: \(\widehat{AB_1}=\widehat{_1By'}=\frac{\widehat{ABy'}}{2}\)(3)
Từ (1), (2) và (3) suy ra \(\widehat{_1AB}=\widehat{AB_1}\)
Mà hai góc này ở vị trí so le trong nên \(A_1//B_1\)(đpcm)

a) Ta có:
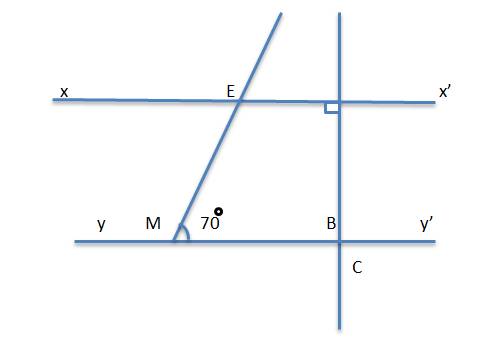
\(xx'\perp C\left(gt\right)\)
\(yy'\perp C\left(gt\right)\)
\(\Rightarrow xx'//yy'\)
b) Ta có: \(xx'//yy'\) và tia \(Mz\) cắt \(xx'\) nên:
\(\widehat{xEM}=\widehat{EMB}\) (so le trong)
\(\Rightarrow\widehat{xEM}=70^o\)
Mà: \(\widehat{xEM}\) đối đỉnh với \(\widehat{zEA}\) nên:
\(\Rightarrow\widehat{zEA}=\widehat{xEM}=70^o\)
\(\widehat{xEz}+\widehat{zEA}=180^o\) (kề bù)
\(\Rightarrow\widehat{xEz}=180^o-70^o=110^o\)
\(\widehat{MEA}+\widehat{xEM}=180^o\) (kề bù)
\(\Rightarrow\widehat{MEA}=180^o-70^o=110^o\)

\(AC//BD\Rightarrow\widehat{CAM}=\widehat{DBM}\)
\(M\)trung điểm \(AB\Rightarrow AM=BM\)
\(\widehat{CMA}=\widehat{DMB}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta CAM=\Delta DBM\left(g.c.g\right)\Rightarrow AC=BD\)

a, Nếu tia At không cắt yy'
=> At // yy'
=> At trung với Ax (vì xx' // yy')
Mà At là phân giác góc xAb
=> At nằm giữa Ax và AB
=> At không trùng Ax
=> At cắt yy'
b,
Bạn xem lại đề. C ở đâu vậy?