Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có 3cosα – sinα = 1 nên 3cosα = sinα + 1
Suy ra: 9cos2α = sin2α + 2sinα + 1
Hay 10sin2α + 2sinα - 8 = 0
Do đó: sinα = -1 hoặc sinα = 0,8
+ sinα = -1 không thỏa mãn vì 00 < α < 900
+ sinα = 0,8 thì cosα = 0,6 và tan α = 0,8 : 0,6 = 4/3.

Ta có 3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.

Ta có:
3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.

Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.
Do đó sinα < (- 2 )/2 và cosα < 2 /2.
Vì vậy sinα + cosα < 0.
Suy ra các phương án A, C, D bị loại.
Đáp án: B

Đáp án B
c o s 2 α = 1 − s i n 2 α = 1 − 12 13 2 = 25 169 .
D o 90 ° < α < 180 ° nên cos α < 0 ⇒ cos α = − 5 13
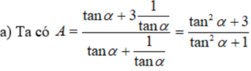
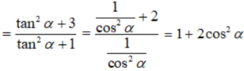
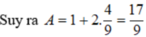

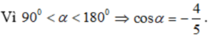
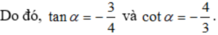


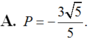

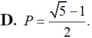
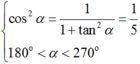
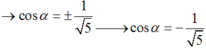
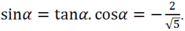
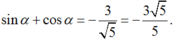
Với 0 ο < α < 90 ο thì 0 < cosα < 1 hay 1/cosα > 1
Nhân hai về với sinα > 0 ta được tanα > sinα
Vậy không có giá trị nào của α ( 0 ο < α < 90 ο ) để tanα < sinα