Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24

Đáp án: B
Sử dụng phương trình Anhxtanh ta được:
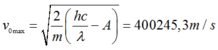
Khi đi vào từ trường mà v 0 ⊥ B thì quang electron chuyển động tròn đều.
Lực Lo - ren - xơ là lực hướng tâm:
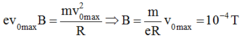

Ta có
Wđ= \(\frac{hc}{\lambda}\)
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)

Công thức Anh-xtanh cho hiện tượng quang điện ngoài
\(hf =A + \frac{1}{2} mv_{0max}^2= A+ W_{đmax}\)
=> \(\frac{hc}{\lambda_1} =\frac{hc}{\lambda_0}+W _{đmax1} \)
=> \(W_{đmax1} = \frac{hc}{\lambda_1} - \frac{hc}{\lambda_0} = 3,011.10^{-19}J.\)
Với công thoát: \(A = \frac{hc}{\lambda_0} = 3.011.10^{-19}J ; \frac{hc}{\lambda_1} = 6,023.10^{-19}J.\)
Mà \(v_{0max2} = \sqrt{2}v_{0max2} => W_{dmax1} = 2W_{dmax2} \)
=> \(\frac{hc}{\lambda_2} =\frac{hc}{\lambda_0}+W _{đmax2} = 3,011.10^{-19} + 6,023.10^{-19} = 9,035.10^{-19}J.\)
=> \(\lambda_2 =\frac{hc}{ \frac{hc}{\lambda_0} +W_{dmax2}} = \frac{6,625.10^{-34}.3.10^8}{9,035.10^{-19}} = 2,2.10^{-7}m = 0,22 \mu m.\)
Chọn đáp án.D. \(0,22\mu m.\)

Áp dụng: \(\varepsilon=A_t+W_đ\)
Năng lượng \(\varepsilon\) tỉ lệ nghịch với bước sóng
Động năng Wđ tỉ lệ thuận với bình phương vận tốc v
Suy ra:
\(\varepsilon =A_t+W_đ\)(1)
\(\dfrac{\varepsilon}{2} =A_t+\dfrac{W_đ}{k^2}\)(2)
\(\dfrac{\varepsilon}{4} =A_t+\dfrac{W_đ}{10^2}\)(3)
Lấy (1) trừ (2) vế với vế: \(\dfrac{\varepsilon}{2} =(1-\dfrac{1}{k^2})W_đ\)(4)
(1) trừ (3):\(\dfrac{3\varepsilon}{4} =\dfrac{99}{100}W_đ\)(5)
Lấy (4) chia (5) vế với vế: \(\dfrac{2}{3}=(1-\dfrac{1}{k^2}).\dfrac{99}{100}\)
\(\Rightarrow k=\sqrt{\dfrac{200}{97}}\)
Giới hạn quang điện \(\lambda_0=\frac{hc}{A}=0,6\mu m\)
Trong ánh sáng trắng có các bước sóng \(\lambda\le\lambda_0\) nên có hiện tượng quang điện xảy ra .
+ \(v_{0max}\) ứng với \(\lambda_{min}=0,4\mu m\):
Từ \(\frac{hc}{\lambda_{min}}=A+\frac{1}{2}mv^2_{0max}\Rightarrow v_{0max}=\)\(\sqrt{\frac{2\left(\frac{hc}{\lambda_{min}}-A\right)}{m}}\)
\(\Leftrightarrow v_{0max}=\sqrt{\frac{\frac{2\left(6,625.10^{-34}.3.10^8\right)}{0,4.10^{-6}}-3,31.10^{-19}}{9,1.10^{-31}}}=\)\(0,6.10^6\left(m\text{/}s\right)\)
cảm ơn nhiều