Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải bài toán bằng cách lập phương trình :1 đoạn thẳng dài 23cm,được chia thành 2 đoạn .trên mỗi đoạn người ta dựng 1 hình vuông .tìm độ dài mỗi đoạn biết tổng diện tích của 2 hình vuông là 265cm^2
Toán lớp 8

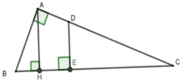
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A

#)Giải :
A B C H
Áp dụng định lí Py - ta - go :
\(BC^2=AB^2+AC^2\Leftrightarrow BC^2=3^2+4^2=9+16=25\)
\(\Rightarrow BC=\sqrt{25}=5\)
Ta có : \(AB.AC=BC.AH\)
\(\Rightarrow3.4=5.AH\Rightarrow H=\frac{12}{5}\)
\(\hept{\begin{cases}AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{3^2}{5}=\frac{9}{5}\\AC^2=BC.CH\Rightarrow CH=\frac{AC^2}{BC}=\frac{4^2}{5}=\frac{16}{5}\end{cases}}\)
Vậy \(\hept{\begin{cases}BC=5\\BH=\frac{9}{15}\\CH=\frac{16}{5}\end{cases}}\)

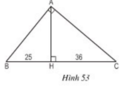
+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
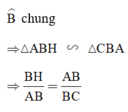
⇒AB2=BH.BC=25.(25+36)=1525