Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

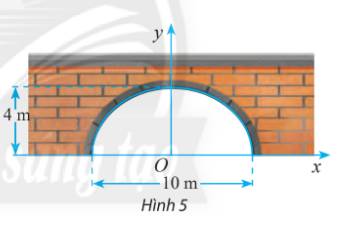
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)
a ) R\(−3;1]=(-∞;-3]∪(1;+∞)
b) [-2; \, 0](−∞;1)\[−2;0]= [-2; \, 0]∞;-2)∪(0;1)

✳️ Giải thích các điều kiện
📌 Điều kiện 1: \(A \subset \mathbb{R} \backslash B\)
- Tức là mọi phần tử của \(A\) không thuộc \(B\) → \(A \cap B = \emptyset\)
- Nghĩa là: Không có phần tử chung giữa \(A = \left(\right. - \infty ; m \left.\right)\) và \(B = \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\)
👉 Điều này xảy ra khi:
\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. = \emptyset\)
→ Tức là:
\(m \leq 3 m + 1\)
Giải bất phương trình:
\(m \leq 3 m + 1 \Rightarrow - 2 m \leq 1 \Rightarrow m \geq - \frac{1}{2}\)
📌 Điều kiện 2: \(A \cap B \neq \emptyset\)
Tức là: phải có phần tử chung giữa \(A = \left(\right. - \infty ; m \left.\right)\) và \(B = \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\)
→ Tức là:
\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. \neq \emptyset\)
→ Điều này xảy ra khi tồn tại \(x \in \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\) sao cho \(x < m\)
→ Nói cách khác:
\(3 m + 1 < m\)
Giải bất phương trình:
\(3 m + 1 < m \Rightarrow 2 m < - 1 \Rightarrow m < - \frac{1}{2}\)
✅ Kết luận
- Từ (1): \(m \geq - \frac{1}{2}\)
- Từ (2): \(m < - \frac{1}{2}\)
⛔ Hai điều kiện mâu thuẫn nhau → Không có giá trị \(m\) nào thỏa mãn đồng thời cả hai điều kiện.

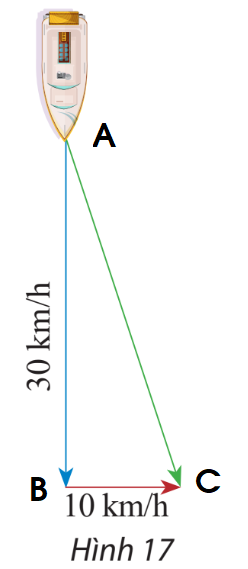
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

a) \(B\subset A\)
\(\Rightarrow\left(-4;5\right)\subset\left(2m-1;m+3\right)\)
\(\Rightarrow2m-1\le-4< 5\le m+3\)
\(\Rightarrow\hept{\begin{cases}2m-1\ge4\\5\le m+3\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}m< -\frac{3}{2}\\m\ge2\end{cases}}\left(ktm\right)\)
\(\Rightarrow m\in\varnothing\)
b) \(A\text{∩ }B=\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m+3< -4\\5< 2m-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}m< -7\\m>3\end{cases}}\)
Vậy \(m< -7;m>3\)