K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LA
0
NT
1
TL
18 tháng 6 2019
Đề thi thử + tính điểm với những đề mới nhất cả nhà tải app dùng thử nhé https://giaingay.com.vn/downapp.html
T
1 tháng 5 2021
ý a dễ
b/ Ta có IM=IN (đề bài) => OI vuông góc AN => ^AIO=90
Ta lại có ^ABO=^ACO=90 (AB,AC là tiếp tuyến)
=> B,I,C đều nhìn AO dưới 1 góc 90 độ => B,I,C cùng nằm trên 1 đường tròn đường kính AO => B,I,C,O cùng nằm trên 1 đường tròn
c/
Ta có AB=AC => số đo cung AB thuộc đường tròn đk AO = số đo cung AC thuộc đường tròn đk AO (1)
số đo ^AIB=1/2 số đo cung AB (góc nội tiếp) (2)
số đo ^AIC=1/2 sso đo cung AC (góc nội tiếp) (3)
Từ (1) (2) và (3) => ^AIB=^AIC => AI là phân giác của góc BIC
1 tháng 5 2021
@Bakura : Câu a với b mình chứng minh được rồi bạn, mình cần câu c. Bạn biết làm câu c thì giúp mình với ạ, cảm ơn bạn.
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
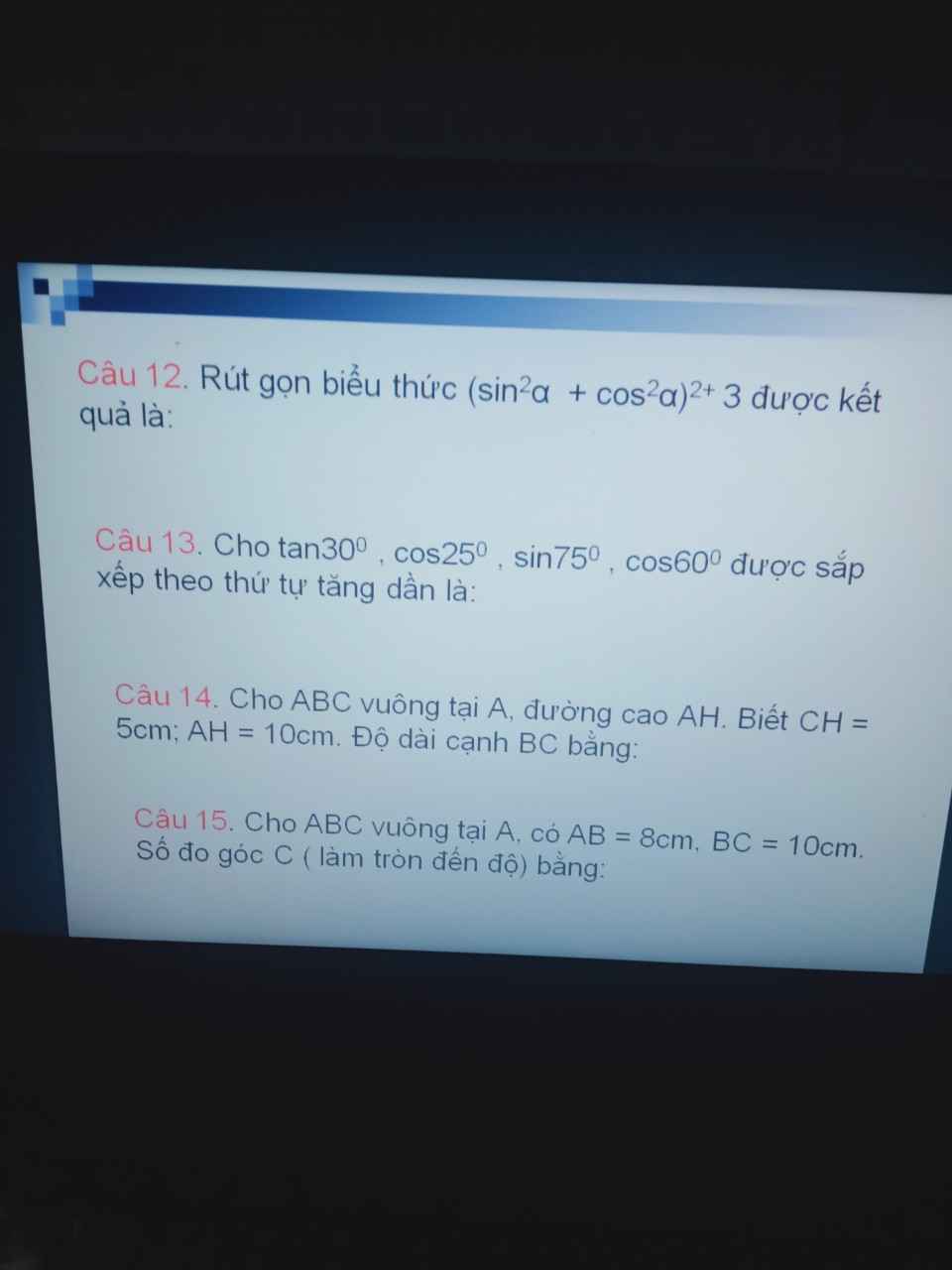
Câu 14:
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH$
$BH=\frac{AH^2}{CH}=\frac{10^2}{5}=20$
$BC=BH+CH=20+5=25$ (cm)
Câu 15:
Áp dụng hệ thức lượng trong tam giác vuông:
$\sin C=\frac{AB}{BC}=\frac{8}{10}=\frac{4}{5}$
$\Rightarrow \widehat{C}=53,13^0$
TM
26 tháng 3 2022
15. Gọi chiều dài là x, chiều rộng là y (x, y > 0).
- 2 lần chiều dài bằng 3 lần chiều rộng \(\Rightarrow2x=3y\left(1\right)\)
- Nửa chu vi bằng 20 (cm) \(\Rightarrow x+y=20\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}2x=3y\\x+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\\dfrac{3y}{2}+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\3y+2y=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3.8}{2}\\y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\left(tmđk\right)\\y=8\left(tmđk\right)\end{matrix}\right.\)
Vậy : ...
1N
1
1 tháng 10 2021
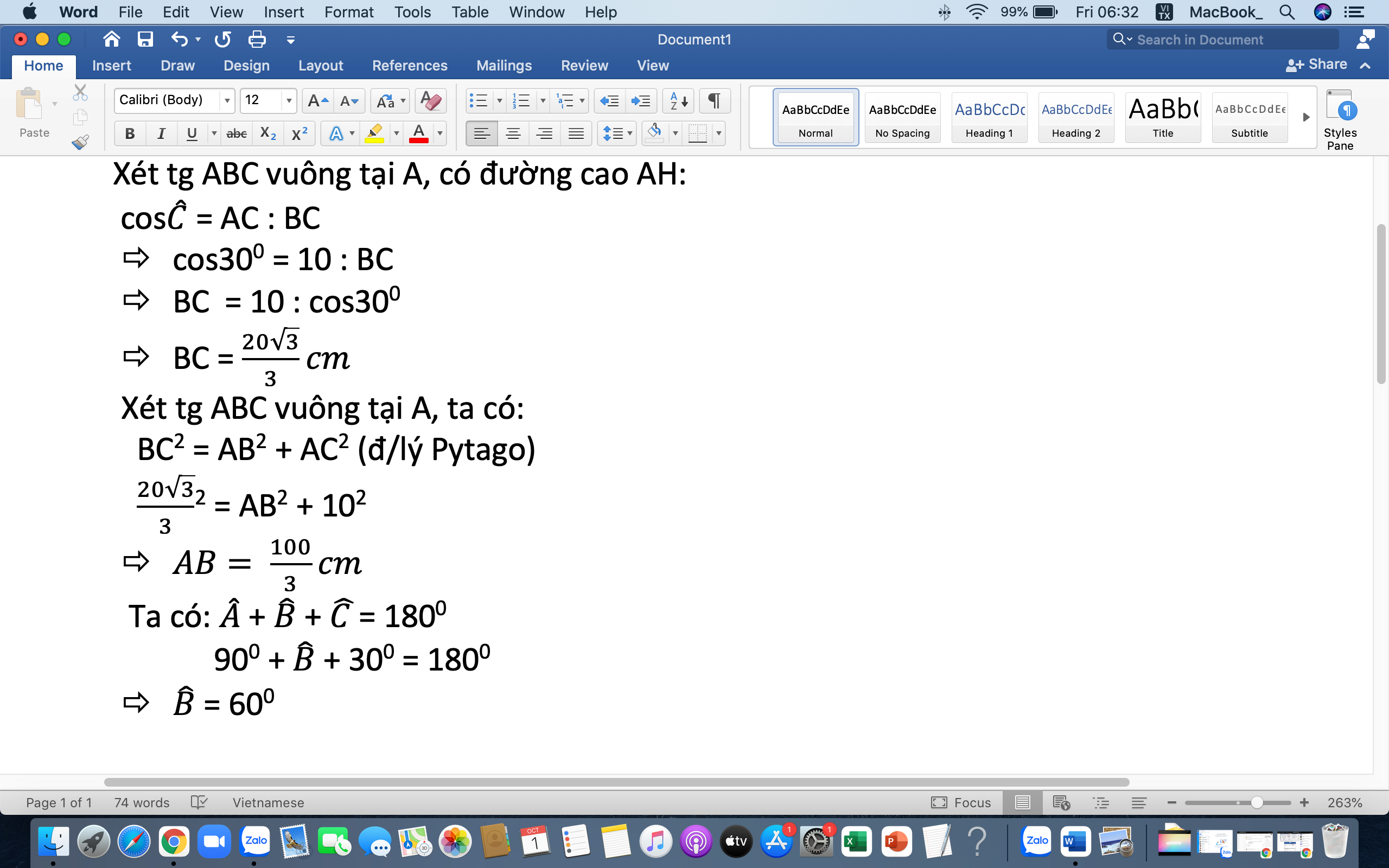
trong \(\Delta ABC\) vuông tại A
AB=AC.tanC=10.tan30=5,77
CB=\(\sqrt{AC^2+AB^2}=\sqrt{10^2+5,77^2}=11,55\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5,77.10}{11,55}=5\)
\(\widehat{B}=90-\widehat{C}=90-30=60\)
