K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 3 2022
\(\lim\dfrac{\sqrt{3n^2+1}+n}{\sqrt{2n^2-3}+n+1}=\lim\dfrac{n\sqrt{3+\dfrac{1}{n^2}}+n}{n\sqrt{2-\dfrac{3}{n^2}}+n+1}\)
\(=\lim\dfrac{n\left(\sqrt{3+\dfrac{1}{n^2}}+1\right)}{n\left(\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}\right)}=\lim\dfrac{\sqrt{3+\dfrac{1}{n^2}}+1}{\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}}=\dfrac{\sqrt{3}+1}{\sqrt{2}+1}\)
VV
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
G
8 tháng 8 2023
d) \(y=4sinx-2cos2x-1\)
\(=4sinx-2\left(1-2sin^2x\right)-1\)
\(=4sin^2x+4sinx-3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=f\left(t\right)=4t^2+4t-3\) \(\Leftrightarrow f'\left(t\right)=8t+4\)
\(f'\left(t\right)=0\Leftrightarrow t=-\dfrac{1}{2}\)
Vẽ BBT với \(t\in\left[-1;1\right]\) ta được
\(minf\left(t\right)=miny=-4\Leftrightarrow t=-\dfrac{1}{2}\)\(\Leftrightarrow sinx=-\dfrac{1}{2}\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) ( k thuộc Z)
\(maxf\left(t\right)=miny=5\Leftrightarrow t=1\)\(\Leftrightarrow sinx=1\) \(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\) ( k thuộc Z)
Vậy...
G
8 tháng 8 2023
e) \(y=3sin2x+8cos^2x-1\)
\(=3sin2x+4\left(2cos^2x-1\right)+3\)
\(=3sin2x+4cos2x+3\)
\(=5\left(\dfrac{3}{5}sin2x+\dfrac{4}{5}cos2x\right)+3\)
Đặt \(cosu=\dfrac{3}{5}\Leftrightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sin2x.cosu+cos2x.sinu\right)+3=5.sin\left(2x+u\right)+3\)
Có \(-1\le sin\left(2x+u\right)\le1\) \(\Leftrightarrow-2\le y\le8\)
\(maxy=8\Leftrightarrow sin\left(2x+u\right)=1\) \(\Leftrightarrow2x+u=\dfrac{\pi}{2}+k2\pi\) \(\Leftrightarrow x=-\dfrac{u}{2}+\dfrac{\pi}{4}+k\pi\)\(\Leftrightarrow x=-\dfrac{1}{2}.arccos\dfrac{3}{5}+\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
\(miny=-2\Leftrightarrow sin\left(2x+u\right)=-1\)\(\Leftrightarrow x=-\dfrac{1}{2}.\dfrac{arccos3}{5}-\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
Vậy...
I
26 tháng 9 2023
a)
\(sinx=sin\dfrac{\pi}{6}\\ < =>\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\pi-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
b)
\(sin2x=\dfrac{\sqrt{3}}{2}\\ < =>sin2x=sin\dfrac{\pi}{3}\\ < =>\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
c)
\(sin\left(x+\dfrac{\pi}{3}\right)=sin\left(2x-\dfrac{\pi}{4}\right)\\ < =>\left[{}\begin{matrix}x+\dfrac{\pi}{3}=2x-\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{3}=\pi-2x+\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{7\pi}{12}-k2\pi\\x=\dfrac{11\pi}{12}+k2\pi\end{matrix}\right.\)
(hiện tại mình vẫn đang trong quá trình làm nhưng do vấn đề thời gian nên mình tạm dừng tại đây)
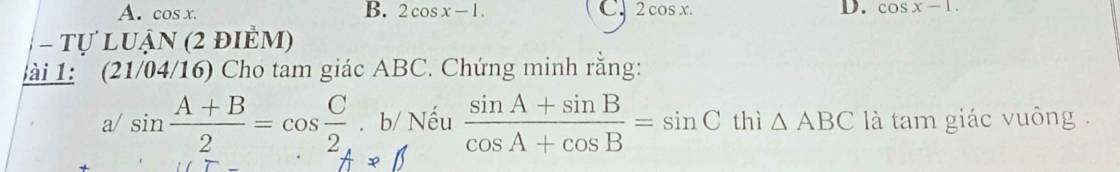
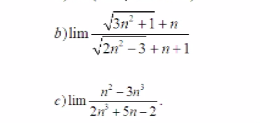
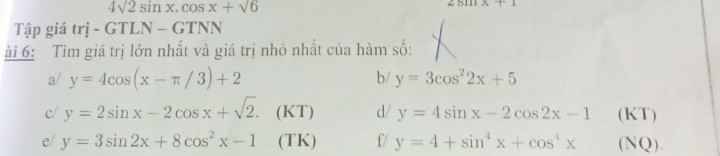
b: \(sinC=\dfrac{sinA+sinB}{cosA+cosB}=\dfrac{2\cdot sin\left(\dfrac{A+B}{2}\right)\cdot cos\left(\dfrac{A-B}{2}\right)}{2\cdot cos\left(\dfrac{A+B}{2}\right)\cdot cos\left(\dfrac{A-B}{2}\right)}\)
=>\(sinC=\dfrac{sin\left(\dfrac{A+B}{2}\right)}{cos\left(\dfrac{A+B}{2}\right)}=\dfrac{sin\left(\dfrac{C}{2}\right)}{cos\left(\dfrac{C}{2}\right)}\)
=>\(2\cdot sin\left(\dfrac{C}{2}\right)\cdot cos\left(\dfrac{C}{2}\right)=sin\left(\dfrac{C}{2}\right)\cdot\dfrac{1}{cos\left(\dfrac{C}{2}\right)}\)
=>\(2\cdot cos^2\left(\dfrac{C}{2}\right)=1\)
=>cos(C)=0
=>góc C=90 độ
=>ΔABC vuông tại C
hình như bị lộn chỗ => đầu tiên kìa bạn