Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tạo độ A là:
\(\left\{{}\begin{matrix}y=0\\-x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-x=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)
Vậy: O(0;0); A(2;0); B(0;2)
\(OA=\sqrt{\left(2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{2^2}=2\)
b: \(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)
Chu vi tam giác OAB là:
\(C_{OAB}=OA+OB+AB=4+2\sqrt{2}\)
Ta có: Ox\(\perp\)Oy
=>OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)

a) Để viết phương trình đường thẳng AB, CD, DA, ta có thể sử dụng công thức phương trình đường thẳng đi qua hai điểm.
Phương trình đường thẳng AB: Điểm A(4,5) và B(1,-1) Ta có: Độ dốc của đường thẳng AB: m = (y2 - y1) / (x2 - x1) = (-1 - 5) / (1 - 4) = -2 Phương trình đường thẳng AB: y - y1 = m(x - x1) => y - 5 = -2(x - 4) => y - 5 = -2x + 8 => 2x + y = 13
Phương trình đường thẳng CD: Điểm C(4,-4) và D(7,-1) Ta có: Độ dốc của đường thẳng CD: m = (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (7 - 4) = 1 Phương trình đường thẳng CD: y - y1 = m(x - x1) => y - (-1) = 1(x - 7) => y + 1 = x - 7 => x - y = 8
Phương trình đường thẳng DA: Điểm D(7,-1) và A(4,5) Ta có: Độ dốc của đường thẳng DA: m = (y2 - y1) / (x2 - x1) = (5 - (-1)) / (4 - 7) = -2 Phương trình đường thẳng DA: y - y1 = m(x - x1) => y - (-1) = -2(x - 7) => y + 1 = -2x + 14 => 2x + y = 13
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh của tứ giác.
Độ dài cạnh AB: AB = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(1 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Độ dài cạnh BC: BC = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(4 - 1)^2 + (-4 - (-1))^2] = √[9 + 9] = √18
Độ dài cạnh CD: CD = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - (-4))^2] = √[9 + 9] = √18
Độ dài cạnh DA: DA = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Từ đó, chu vi tứ giác ABCD là: AB + BC + CD + DA = √45 + √18 + √18 + √45.
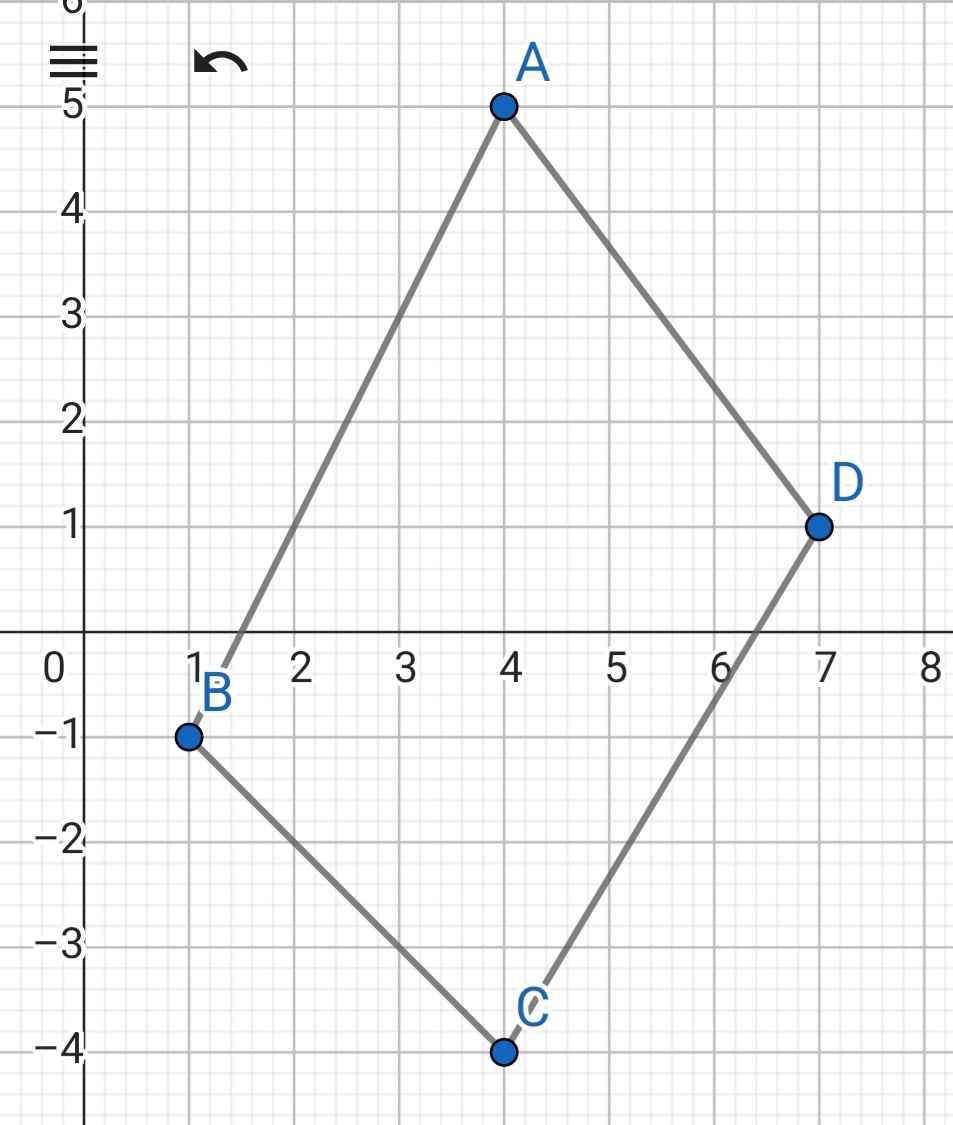 a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
Do (d) đi qua A nên:
4a + b = 5
⇔ b = 5 - 4a (1)
Do (d) đi qua B nên:
a + b = -1 (2)
Thay (1) vào (2) ta được:
a + 5 - 4a = -1
⇔ -3a = -6
⇔ a = 2
Thay a = 2 vào (1) ta được:
b = 5 - 4.2 = -3
Vậy (d): y = 2x - 3
* Gọi (d'): y = ax + b là phương trình đường thẳng CD
Do (d') đi qua C nên:
4a + b = -4
⇔ b = -4 - 4a (3)
Do (d') đi qua D nên:
7a + b = -1 (4)
Thay (3) vào (4) ta được:
7a - 4 - 4a = -1
⇔ 3a = 3
⇔ a = 1
Thay a = 1 vào (3) ta được:
b = -4 - 4.1 = -8
Vậy (d'): y = x - 8
* Gọi (d''): y = ax + b là phương trình đường thẳng DA
Do (d'') di qua D nên:
7a + b = -1
⇔ b = -1 - 7a (5)
Do (d'') đi qua A nên:
4a + b = 5 (6)
Thay (5) vào (6) ta được:
4a - 1 - 7a = 5
⇔ -3a = 6
⇔ a = -2
Thay a = -2 vào (5) ta được:
b = -1 - 7.(-2) = 13
Vậy (d''): y = -2x + 13
b) Ta có:
AB² = 3² + 6² = 45
⇒ AB = 3√5
BC² = 3² + 3² = 18
⇒ BC = 3√2
CD² = 3² + 5² = 34
⇒ CD = √34
AD² = 3² + 4² = 25
⇒ AD = 5
Chu vi tứ giác ABCD:
3√5 + 3√2 + √34 + 5

a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
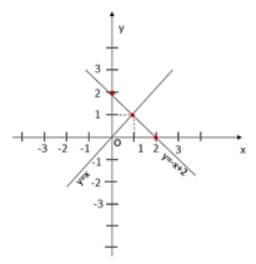
b) Giao điểm A của hai đường thẳng đã cho là A(1;1)
c) Cho y =0 ta được −x + 2 = 0 hay x = 2, suy ra B(2; 0).
Gọi C là giao điểm của đường thẳng y = −x + 2 và trục Oy. Suy ra C(0; 2). Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).
Xét hai tam giác OAB và OAC có:
cạnh OA chung;
OB = OC;
\( \widehat {OBA} = \widehat {OCA} = 45^0\)
Do đó \(\Delta OAB = \Delta OAC\), từ đó suy ra AB = AC.
Điều này chứng tỏ A là trung điểm của BC, mà \(\Delta OBC \) cân tại O nên \(OA \bot AB\), tức là \(\Delta OAB\) vuông tại A.
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1

a: A(0;4); B(-3;0); C(3;0)
\(AB=\sqrt{\left(-3-0\right)^2+\left(0-4\right)^2}=5\)
\(AC=\sqrt{\left(3-0\right)^2+\left(0-4\right)^2}=5\)
\(BC=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
Chu vi tam giác ABC là:
5+5+6=16
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5^2+5^2-6^2}{2\cdot5\cdot5}=\dfrac{7}{25}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{25}\right)^2}=\dfrac{24}{25}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(\dfrac{1}{2}\cdot5\cdot5\cdot\dfrac{24}{25}=\dfrac{24}{2}=12\)
b: Khoảng cách từ C đến AB là:
\(2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot12}{5}=\dfrac{24}{5}=4,8\)

Lời giải:
Gọi B(a,b)B(a,b) và C(c,d)C(c,d)
Ta có HA−→−=(0,4)⊥BC−→−=(c−a,d−b)⇒4(d−b)=0→b=dHA→=(0,4)⊥BC→=(c−a,d−b)⇒4(d−b)=0→b=d
Thay d=bd=b:
HB−→−=(a−1,b−2)⊥AC−→−=(c−1,b−6)HB→=(a−1,b−2)⊥AC→=(c−1,b−6)
⇒(a−1)(c−1)+(b−2)(b−6)=0⇒(a−1)(c−1)+(b−2)(b−6)=0
Lại có IA2=IB2=IC2↔
∆OAB vuông tại O
⇒ AB² = OA² + OB² (Pythagore)
= 3² + 4²
= 25
⇒ AB = 5
⇒ Chu vi ∆OAB:
OA + OB + AB = 3 + 4 + 5 = 12