Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1
\(Q=16,8kJ=16800J\)
\(m=2kg\)
\(\Delta t=20^0C\)
__________
\(c=?J/kg.K\)
Giải
Nhiệt dung riêng của chất này là:
\(Q=m.c.\Delta t\Rightarrow c=\dfrac{Q}{m.\Delta t}=\dfrac{16800}{2.20}=420J/kg.K\)
Câu 2
Tóm tắt
\(m=50kg\)
\(\Rightarrow P=10.m=10.50=500N\)
\(h=20m\)
_________
\(F=?N\)
\(s=?m\)
\(A=?J\)
Giải
Vì dùng ròng rọc động nên:
Lực kéo là:
\(F=\dfrac{P}{2}=\dfrac{500}{2}=250N\)
Quãng đường sọi dây của ròng rọc di chuyển là:
\(s=h.2=20.2=40m\)
Công thực hiện được là:
\(A=F.s=250.40=10000\left(J\right)\)

sửa : 20C =2oC
nhiệt dung riêng của chất này là
\(Q=m.c.\Delta t\Rightarrow c=\dfrac{Q}{\Delta t.m}=\dfrac{8400}{2.1}=4200\)J/kg.K
vậy chất cần tìm là nước
c=\(\dfrac{Q}{m.t}=\dfrac{8400}{1.20}=420\left(\dfrac{J}{kg.K}\right)\)?

Để tính nhiệt dung riêng của hỗn hợp chất lỏng, ta có thể sử dụng định luật bảo toàn năng lượng.
Giả sử hai khối chất lỏng có nhiệt dung riêng lần lượt là c1 và c2. Khi cung cấp một lượng nhiệt lượng q2, ta tìm được nhiệt độ tăng như nhau cho cả hai chất lỏng.
Khi nhập hai khối chất lỏng và cung cấp một lượng nhiệt lượng q, ta cũng tìm được nhiệt độ tăng như trên.
Theo định luật bảo toàn năng lượng, tổng năng lượng của hỗn hợp chất lỏng trước và sau khi cung cấp nhiệt lượng q phải bằng nhau.
Năng lượng ban đầu của hỗn hợp chất lỏng là q, và năng lượng cuối cùng của hỗn hợp chất lỏng là q1 + q2 (với q1 là nhiệt lượng cung cấp cho chất lỏng thứ nhất).
Vì tổng năng lượng không thay đổi, ta có:
q = q1 + q2
Với q1 = c1 * ΔT1 (với ΔT1 là sự tăng nhiệt độ của chất lỏng thứ nhất) và q2 = c2 * ΔT2 (với ΔT2 là sự tăng nhiệt độ của chất lỏng thứ hai).
Do đó, ta có:
q = c1 * ΔT1 + c2 * ΔT2
Để tính nhiệt dung riêng của hỗn hợp chất lỏng, ta cần biết giá trị của ΔT1 và ΔT2. Từ đó, ta có thể tính được nhiệt dung riêng của hỗn hợp chất lỏng bằng cách sắp xếp lại công thức trên:
c_mix = q / (ΔT1 + ΔT2)
Với c_mix là nhiệt dung riêng của hỗn hợp chất lỏng.
Lưu ý rằng giá trị của ΔT1 và ΔT2 phải được xác định từ dữ liệu cụ thể của bài toán hoặc thông qua các phép đo thí nghiệm.

a/ Giả sử rằng, thoạt đầu ta trộn hai chất có nhiệt độ thấp hơn với nhau ta thu được một hỗn hợp ở nhiệt độ t < t3 ta có pt cân bằng nhiệt:
m1C1(t1 - t) = m2C2(t - t2)
\(t=\frac{m_1c_1t_1+m_2c_2t_2}{m_1c_1+m_2c_2}\left(1\right)\) (1)
Sau đó ta đem hỗn hgợp trên trôn với chất thứ 3 ta thu được hỗn hợp 3 chất ở nhiệt độ t' (t < t' < t3) ta có phương trình cân bằng nhiệt:
(m1C1 + m2C2)(t' - t) = m3C3(t3 - t') (2)
Từ (1) và (2) ta có:
\(t'=\frac{m_1c_1t_1+m_2c_2t_2+m_3c_3t_3}{m_1c_1+m_2c_2+m_3c_3}\)
Thay số vào ta tính được t' ≈ -190C
b/ Nhiệt lượng cần thiết để nâng nhiệt độ của hỗn hợp lên 60C:
Q = (m1C1 + m2C2 + m3C3) (t4 - t') = 1300000(J)

Q(cung cấp)= 0,27(kJ)=270(J)
<=> m.c. \(\Delta t\) = 270
<=> 0,1.c.1,5=270
<=>c=1800(J/kg.K)
=> Chất này là nước đá

1) Một quả cầu đặc bằng đồng nặng 3,2 kg đang ở nhiệt độ 200C. Để nhiệt độ của quả cầu tăng lên đến 750C thì cần cung cấp nhiệt lượng bao nhiêu? Cho cđ = 380 J/kg.K
Tóm tắt :
m = 3,2 kg
t1 = 20oC
c = 380 J/kg.K
t2 = 75oC
Q = ? J
Giải :
Theo CT : Q = m . c . \(\Delta\)t = 3,2 . 380 . (t2 - t1) = 66880 J
Đáp số : 66880 J
2) Cung cấp một nhiệt lượng Q = 378 kJ cho 2 kg nước ở 350C. Tìm nhiệt độ sau cùng của nước. Biết cn = 4200 J/kg.K và bỏ qua sự trao đổi nhiệt của môi trường bên ngoài.
Tóm tắt :
Q = 378 kJ = 378000 J
m = 2kg
t1 = 35oC
c = 4200 J/kg.K
t2 = ? oC
Giải :
Theo CT : Q = m . c . Δt
=> Δt = \(\dfrac{Q}{m.c}=\) \(\dfrac{378000}{2.4200}=45^oC\)
Δt = t2 - t1 => t2 = Δt + t1 = 45 + 35 = 80oC
Đáp số : 80oC
1)
Q tỏa ra = Q thu vào = 3,2.380.(75-20)=66880j
Vậy cần 66880j để làm nóng quả cầu đặc bằng đồng đang ở 20độ lên 75độ
2)
378kj=378000j
Q tỏa ra = Q thu vào =378000j
=>t2-35=378000:(2.4200)=45
=>t2=35độ +45độ=80độ
Vậy nhiệt độ sau cùng của nước là 80 độ C
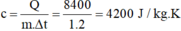
Tóm tắt:
\(Q=16,8kJ=16800J\)
\(m=2kg\)
\(\Delta t=2^oC\)
__________________________
\(c=?\)
Giải
Nhiệt dung riêng của chất này là:
\(Q=m.c.\Delta t\Rightarrow c=\dfrac{Q}{m.\Delta t}=\dfrac{16800}{2.2}=4200\left(J/kgK\right)\)
→ Chất này là nước.
Tóm tắt:
\(Q=16,8kJ=16800J\)
\(m=2kg\)
\(\Delta t=2^oC\)
==========
\(c=?J/kg.K\)
Nhiệt dung riêng của chất này là:
\(Q=m.c.\Delta t\Rightarrow c=\dfrac{Q}{m.\Delta t}=\dfrac{16800}{2.2}=4200J/kg.K\)
Vậy chất này là nước