Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vận tốc truyền tải v = x 2 ln 1 x với
0 < x < 1 ⇒ v ' = − x 2 ln x + 1 ⇒ v ' = 0 ⇔ x = 0 x = 1 e
Dựa vào bảng biến thiên, suy ra v đạt giá trị lớn nhất khi x = 1 e = 2 h ⇔ h = 2 e .

*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2

Đáp án C
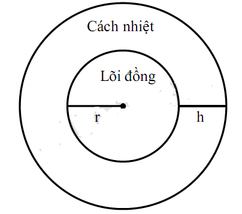
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13

Tóm tắt:
s1 = s2
v1 = 15 km/h
v2 = 10 km/h
__________
vtb = ? (km/h)
Giải:
Thời gian trên nửa quãng đường đầu:
\(v_1=\frac{s_1}{t_1}\Rightarrow t_1=\frac{s_1}{v_1}=\frac{s_1}{15}\left(h\right)\)
Thời gian trên nửa quãng đường sau:
\(v_2=\frac{s_2}{t_2}\Rightarrow t_2=\frac{s_2}{v_2}=\frac{s_1}{10}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường AB:
\(v_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{s_1+s_1}{\frac{s_1}{15}+\frac{s_1}{10}}=\frac{2s_1}{s_1\left(\frac{1}{15}+\frac{1}{10}\right)}=\frac{2}{\frac{1}{6}}=12\) (km/h)
ĐS: 12 km/h
tóm tắt: v1=15km/h BL
v2=10km/h Vận tốc trung bình người đó đi trên cả quãng đường AB là:
vtb=? vtb=( 2*v1*v2 ) / ( v1 + v2) =(2*15*10) / (15+10)=12 km/h
Vậy vận tốc trung bình trên cả quãng đường AB là 12 km/h
Đáp án C
Ta có: v = x 2 ln 1 x = − x 2 ln x
⇒ v ' = − 2 x ln x + x 2 . 1 x = 0 ⇔ x = 0 l o a i ln x = − 1 2 ⇒ x = 1 e
Lại có: lim x → 0 v = lim x → 1 v = 0 ; f 1 e = 1 2 e
⇒ M ax 0 ; 1 v = 1 2 e k h i x = 1 e = r h = 2 h ⇒ h = 2 e .