K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 10 2021
a)Đk \(x\ge0,x\ne1\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
8 tháng 10 2021
b)\(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\Rightarrow\sqrt{x}=2-\sqrt{3}\)
\(\Rightarrow P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2-\sqrt{3}-1}{2-\sqrt{3}+1}=\dfrac{1-\sqrt{3}}{3-\sqrt{3}}=\dfrac{-\sqrt{3}}{3}\)
DH
1
30 tháng 9 2021
1)
\(\left[\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1}\right]:\dfrac{2\sqrt{3x}}{x-1}\)
\(=\left(\dfrac{x+\sqrt{x}+x-\sqrt{x}}{x-1}\right).\dfrac{x-1}{2\sqrt{3x}}\)
\(=\dfrac{2x}{x-1}.\dfrac{x-1}{2\sqrt{3x}}=\dfrac{\sqrt{x}}{\sqrt{3}}=\dfrac{\sqrt{3x}}{3}\)
LD
7 tháng 7 2018
Có A = x - căn x = x - căn x + 1/4 -1/4 = ( căn x - 1/2)2- 1/4 >= -1/4
Dấu "=" xáy ra <-> x = 1/4
Vậy min của A là -1/4 <-> x= 1/4
HL
1
MH
20 tháng 8 2016
\(3+\sqrt{2x-3}=x\) (ĐKXĐ: x \(\ge\)1,5)
\(\Leftrightarrow\sqrt{2x-3}=x-3\)
\(\Leftrightarrow2x-3=x^2-6x+9\)
\(\Leftrightarrow-x^2+8x-12=0\)
\(\Leftrightarrow-\left(x^2-8x+12\right)=0\)
\(\Leftrightarrow x^2-6x-2x+12=0\)
\(\Leftrightarrow x.\left(x-6\right)-2.\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x-2\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x=6\\x=2\end{cases}\left(\text{TMĐK}\right)}\)
Vậy ...
19 tháng 8 2021
Ta có: \(6\sqrt{2}+\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\)
\(=\dfrac{12+\sqrt{12-2\sqrt{11}}-\sqrt{12+2\sqrt{11}}}{\sqrt{2}}\)
\(=\dfrac{12+\sqrt{11}-1-\sqrt{11}-1}{\sqrt{2}}\)
\(=5\sqrt{2}\)
NT
0
HT
0
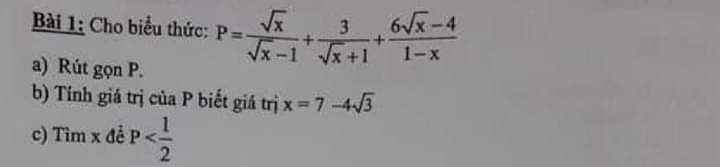
\(\sqrt{x^2-10x+25}-3=0\)\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=3\)\(\Leftrightarrow\left|x-5\right|=3\)(*)
Trường hợp \(x\ge5\)thì (*) \(\Leftrightarrow x-5=3\Leftrightarrow x=8\left(nhận\right)\)
Trường hợp \(x< 5\)thì (*) \(\Leftrightarrow5-x=3\Leftrightarrow x=2\left(nhận\right)\)
Vậy phương trình đã cho có tập nghiệm \(S=\left\{2;8\right\}\)