K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 3 2021
Bài 5:
Ta có: \(\dfrac{158-x}{31}+\dfrac{185-x}{29}+\dfrac{208-x}{27}+\dfrac{227-x}{25}=10\)
\(\Leftrightarrow\dfrac{158-x}{31}+\dfrac{185-x}{29}+\dfrac{208-x}{27}+\dfrac{227-x}{25}-10=0\)
\(\Leftrightarrow\dfrac{158-x}{31}-1+\dfrac{185-x}{29}-2+\dfrac{208-x}{27}-3+\dfrac{227-x}{25}-4=0\)
\(\Leftrightarrow\dfrac{127-x}{31}+\dfrac{127-x}{29}+\dfrac{127-x}{27}+\dfrac{127-x}{25}=0\)
\(\Leftrightarrow\left(127-x\right)\left(\dfrac{1}{31}+\dfrac{1}{29}+\dfrac{1}{27}+\dfrac{1}{25}\right)=0\)
mà \(\dfrac{1}{31}+\dfrac{1}{29}+\dfrac{1}{27}+\dfrac{1}{25}>0\)
nên 127-x=0
hay x=127
Vậy: S={127}
15 tháng 10 2021
Bài 2:
Ta có: \(2\left(5m+2\right)^2-8\)
\(=2\cdot\left(25m^2+20m+4\right)-8\)
\(=50m^2+40m\)
\(=10m\left(5m+4\right)⋮10\)
21 tháng 10 2021
Bài 4:
b: \(B=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3-5-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3-y^3+2y^3-5-x^3-y^3\)
=-5
c: \(C=\left(x-1\right)^3-\left(x+1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6\left(x^2-1\right)\)
\(=-6x^2-2-6x^2+6\)
\(=-12x^2+4\)
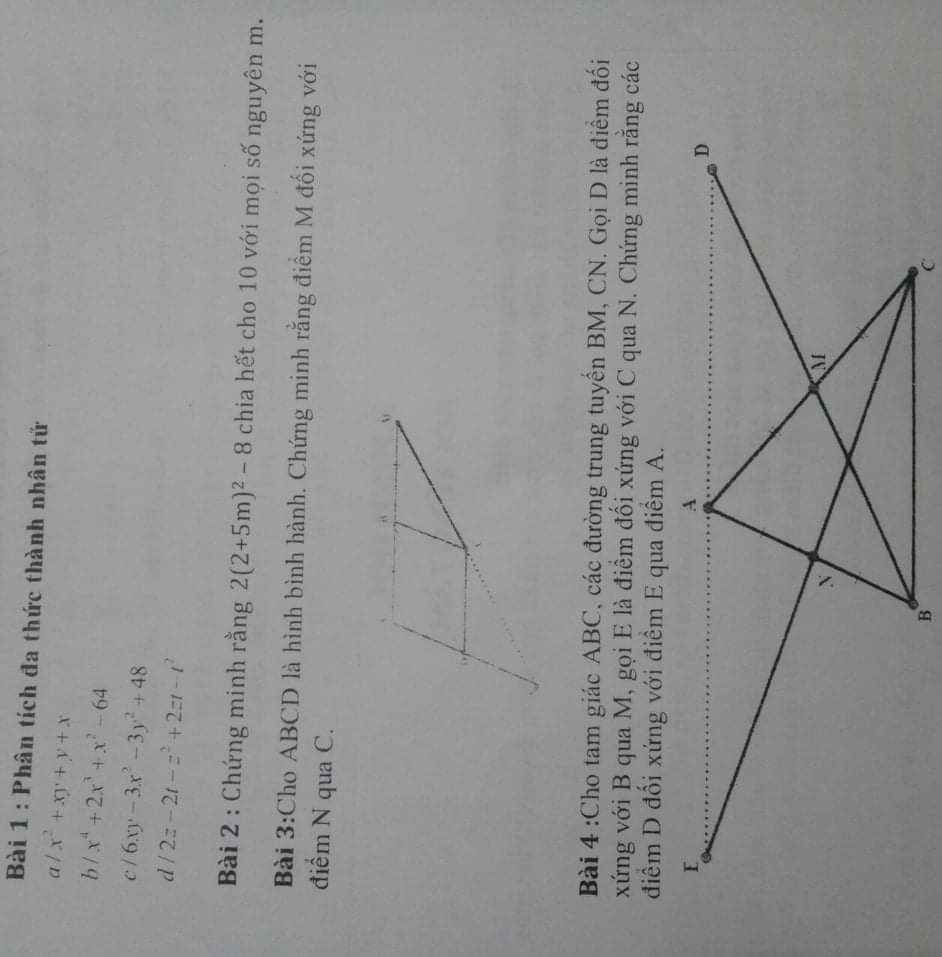
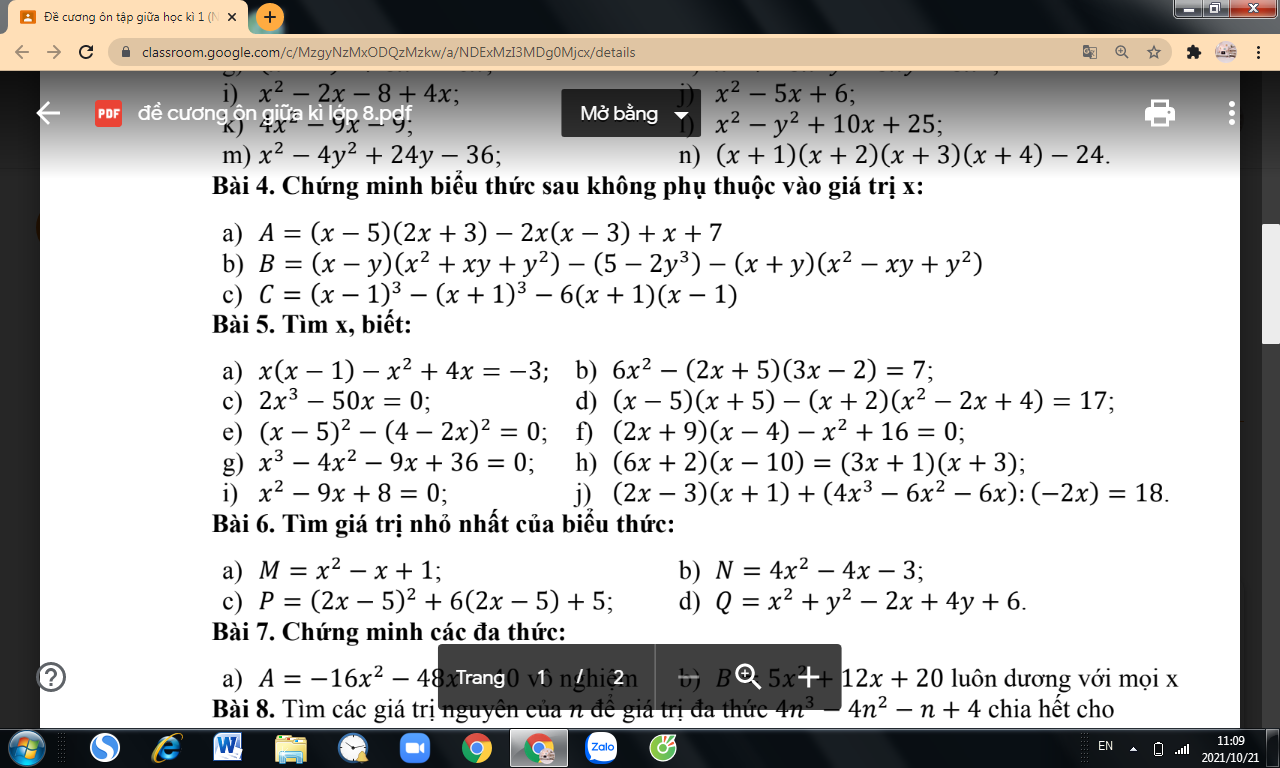
Giúp mik bài 4 vs mn, mik đag cần gấp
làm hộ e bài 4 ạ,e đang cần gấp
\(4,\\ a,=\left(x-3\right)^2\\ b,=\left(3x+1\right)^2\\ c,=\left(5x-3y\right)\left(5x+3y\right)\\ d,=\left(x-2\right)\left(x^2+2x+4\right)\\ e,=\left(2x+1\right)\left(4x^2-2x+1\right)\\ f,=\left(x-3\right)^3\\ g,=\left(a+b-1\right)^2\\ h,=\left(a+2\right)^3\\ i,=\left(x^2+4-4x\right)\left(x^2+4+4x\right)=\left(x-2\right)^2\left(x+2\right)^2\\ u,=\left(x+y+z-2z\right)\left(x+y+z+2z\right)\\ =\left(x+y-z\right)\left(x+y+3z\right)\)
\(5,\\ a,=\left(x+y\right)^2=\left(2004-2003\right)^2=1^2=1\\ b,=\left(x+4\right)^3=\left(-4+4\right)^3=0^3=0\)