K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giải theo cách lớp 6 ạ ! Cần gấp nha !!!!
H
30 tháng 6 2017
Giải:
Có:
\(S=\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)+4^3\)
Ta nhân thấy rằng trong tích \(\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)\) có một thừa số bằng 0, đó là thừa số \(2018-2018\)
Mà trong một tích, nếu có một thừa số bằng 0 thì tích đó bằng 0
\(\Leftrightarrow\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)=0\)
\(\Leftrightarrow S=\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)+4^3=0+4^3=4^3=64\)
Vậy \(S=64\)
Chúc bạn học tốt!
AT
30 tháng 6 2017
S= (2018-1)(2018-2) .... (2018-2017) . 0 +43
=> S= 0 + 43 (Trong 1 tích có 1 thừa số bằng 0 thì tích đó bằng 0);
=>S= 4.4.4=64;
Vậy S=64
NT
1
15 tháng 12 2023
k: \(\left(4x-16\right)\left(-72+9x\right)=0\)
=>\(4\cdot\left(x-4\right)\cdot9\left(x-8\right)=0\)
=>\(36\left(x-4\right)\left(x-8\right)=0\)
=>\(\left(x-4\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=8\end{matrix}\right.\)
m: \(\left(20+5x\right)\left(4x-8\right)=0\)
=>\(5\cdot\left(x+4\right)\cdot4\left(x-2\right)=0\)
=>\(\left(x+4\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
n: \(\left(-4x+48\right)\left(2x-24\right)=0\)
=>\(-4\left(x-12\right)\cdot2\left(x-12\right)=0\)
=>\(\left(x-12\right)^2=0\)
=>x-12=0
=>x=12
o: \(\left(4x+16\right)\left(-2x+20\right)\left(-40+x\right)=0\)
=>\(4\cdot\left(x+4\right)\cdot\left(-2\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left(x+4\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-10=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=10\\x=40\end{matrix}\right.\)
p: \(\left(-5x+40\right)\left(-x+2023\right)\left(2x-2\right)=0\)
=>\(-5\left(x-8\right)\cdot\left(-1\right)\cdot\left(x-2023\right)\cdot2\left(x-1\right)=0\)
=>\(\left(x-8\right)\left(x-2023\right)\left(x-1\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x-1=0\\x-2023=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=1\\x=2023\end{matrix}\right.\)
q: \(2024x\left(4x-8\right)\left(5+5x\right)=0\)
=>\(x\cdot4\left(x-2\right)\cdot5\left(x+1\right)=0\)
=>\(x\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-1\end{matrix}\right.\)
r: \(-4x\left(3x+9\right)\left(2x-16\right)=0\)
=>\(-4x\cdot3\left(x+3\right)\cdot2\left(x-8\right)=0\)
=>\(x\left(x+3\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+3=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=8\end{matrix}\right.\)
s: \(\left(-100+5x\right)\left(2x-10\right)\left(6x+6\right)=0\)
=>\(5\cdot\left(x-20\right)\cdot2\left(x-5\right)\cdot6\left(x+1\right)=0\)
=>\(\left(x-20\right)\left(x-5\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-20=0\\x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=5\\x=-1\end{matrix}\right.\)
t: \(\left(-2x+4\right)\left(2x+16\right)\cdot\left(7-x\right)=0\)
=>\(-2\left(x-2\right)\cdot2\left(x+8\right)\cdot\left(-1\right)\cdot\left(x-7\right)=0\)
=>\(\left(x-2\right)\left(x+8\right)\left(x-7\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x-7=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-8\\x=7\end{matrix}\right.\)
NT
1
LM
Lê Minh Vũ
CTVHS
31 tháng 7 2021
\(\frac{-5}{6}\)\(+\)\(\frac{4}{9}\)\(\times\)\(\left(\frac{5}{4}-\frac{2}{3}\right)\)\(\times\)\(\left(-3\right)^2\)\(+\)\(\frac{5}{9}\)\(\times\)\(30\%\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{4}{9}\)\(\times\)\(\frac{7}{12}\)\(\times\)\(9\)\(+\)\(\frac{5}{9}\)\(\times\)\(\frac{3}{10}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{7}{3}\)\(+\)\(\frac{5}{9}\)\(\times\)\(\frac{3}{10}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{7}{3}\)\(+\)\(\frac{1}{6}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{1}{6}\)\(+\)\(\frac{7}{3}\)
\(=\)\(\frac{-2}{3}\)\(+\)\(\frac{7}{3}\)
\(=\)\(\frac{5}{3}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 8 2018
Gọi số cần tìm là \(\overline{abcde}\); Số viết thêm là f
\(\Rightarrow\overline{abcdef}=3.\overline{fabcde}\Rightarrow10.\overline{abcde}+f=300000.f+\overline{abcde}\)
\(\Rightarrow7.\overline{abcde}=299999.f\Rightarrow\overline{abcde}=42857\)
\(\Rightarrow f=\left\{1;2\right\}\)
+ Với \(f=1\Rightarrow\overline{abcde}=42857\)
+ Với \(f=2\Rightarrow\overline{abcde}=85714\)
Thử lại chắc chắn đúng. Tự làm nốt nhé
HH
26 tháng 6 2017
1. Ta có: \(16^{30}=\left(2^4\right)^{30}=2^{120}\)
Mà \(2^{120}< 3^{120}< 3^{121}\)
\(\Rightarrow2^{120}< 3^{121}\)
\(\Rightarrow16^{30}< 3^{121}\)
2. Ta có: \(5^{22}=5^{2.11}=\left(5^2\right)^{11}=25^{11}\)
Vì 25 < 64 nên \(25^{11}< 64^{29}\)
Vậy \(5^{22}< 64^{29}\)
3. Ta có: \(8^{120}=\left(2^3\right)^{120}=2^{360}\)
\(64^{29}=\left(2^6\right)^{29}=2^{174}\)
Vì 360 < 174 nên \(2^{360}< 2^{174}\)
Vậy \(8^{120}>64^{29}\)
4. Ta có: \(333^{444}=\left(333^4\right)^{111}\) \(=\left(111^4.3^4\right)^{111}=\left(111^4.81\right)^{111}\)
\(444^{333}=\left(444^3\right)^{111}\) \(=\left(111^3.4^3\right)^{111}=\left(111^3.64\right)^{111}\)
Vì \(111^4.81>111^3.64\) nên \(\left(111^4.81\right)^{111}>\left(111^3.64\right)^{111}\)
Vậy \(333^{444}>444^{333}\)
26 tháng 6 2017
ban tra loi hoi cham , sang nay thay mk giai roi . Nhung ma mk se tick cho ban nhe !
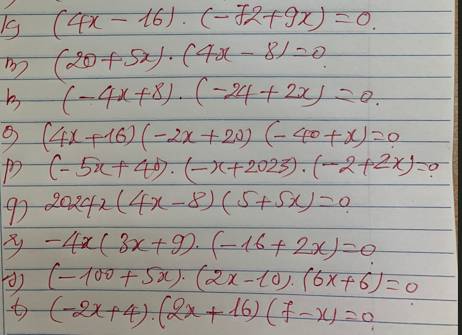
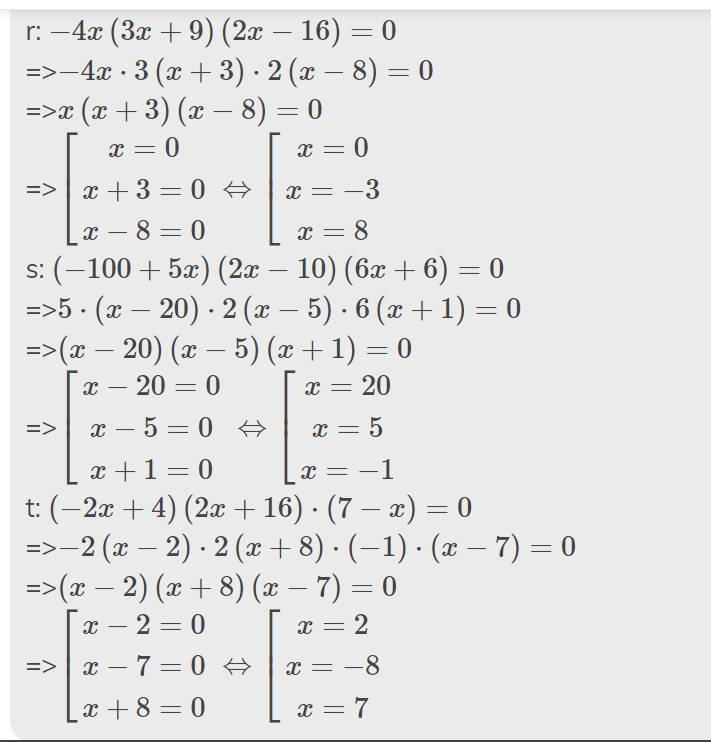
\(\frac{\frac{3}{11}-\frac{3}{13}+\frac{3}{17}-\frac{3}{19}}{\frac{4}{11}-\frac{4}{13}+\frac{4}{17}-\frac{4}{19}}\)
\(=\frac{3.\left(\frac{1}{11}-\frac{1}{13}+\frac{1}{17}-\frac{1}{19}\right)}{4.\left(\frac{1}{11}-\frac{1}{13}+\frac{1}{17}-\frac{1}{19}\right)}\)
\(=\frac{3}{4}\)