Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(\left(x-2\right)\left(\frac{x+1}{3}-x+1\right)=0\)
\(\Leftrightarrow\frac{x\left(x+1\right)}{3}-x^2+x-\frac{2\left(x+1\right)}{3}+2x-2=0\)
\(\Leftrightarrow\frac{x\left(x+1\right)}{3}-x^2+3x-\frac{2\left(x+1\right)}{3}-2=0\)
\(\Leftrightarrow x\left(x+1\right)-3x^2+9x-2\left(x+1\right)-6=0\)
\(\Leftrightarrow x^2+x-3x^2+9x-2x-2-6=0\)
\(\Leftrightarrow-2x^2+8x-8=0\)
\(\Leftrightarrow-2\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow-2.\left(x^2-2.x.2+2^2\right)=0\)
\(\Leftrightarrow-2\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy nghiệm của phương trình là: {2}
2) \(\left(3x+4x\right)\left(\frac{x}{2}-x-\frac{3x}{5}+1\right)=0\)
\(\Leftrightarrow7x\left(\frac{x}{2}-x-\frac{3x}{5}+1\right)=0\)
\(\Leftrightarrow7x\left(-\frac{11x}{10}+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}7x=0\\-\frac{11x}{10}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{11}{10}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{10}{11}\end{cases}}\)
Vậy: nghiệm của phương trình là: \(\left\{0;\frac{10}{11}\right\}\)
3) \(\left|x-1\right|=x^2-x\)
\(\Leftrightarrow x-1=x^2-x\)
\(\Leftrightarrow1=x^2-x-x\)
\(\Leftrightarrow1=x^2\)
\(\Leftrightarrow x^2=1\)
\(\Rightarrow x=\pm1\)
Vậy nghiệm phương trình là: {1; -1}
4) \(\left|x^2-3x+1\right|=2x-3\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-3x+1=2x-3\\x^2-3x+1=-\left(2x-3\right)\end{cases}}\)
Xét trường hợp này rồi làm tiếp, dễ rồi :))

ĐK: \(3-2x\ge0\Leftrightarrow x\le\frac{3}{2}\)
Khi đó; \(\left|2x-3\right|=3-2x\text{ (do }2x-3\le0\text{)}\)
\(pt\Leftrightarrow8+3-2x=2\sqrt{3-2x}\Leftrightarrow\left(\sqrt{3-2x}\right)^2-2\sqrt{3-2x}+1=-7\)
\(\Leftrightarrow\left(\sqrt{3-2x}-1\right)^2=-7\text{ (vô nghiệm)}\)

Xe máy thứ nhất 1 giờ đi được 1/4 quảng đường
Xe máy thứ hai 1 giờ đi được 1/3 quảng đường
Sau 1,5 giờ 2 xe đi được:(1/4+1/3)x1,5=7/12x3/2=7/8(quảng đường)
quảng đường AB là:
15x8=120(km)

Xét 2 trường hợp:
x >= 1 ==> x-1 >= 0 ==>\(\left|x-1\right|=x-1\)
do đó ta có hpt:\(\left\{{}\begin{matrix}x-2y=-5\\y=2.\left(x-1\right)+3\end{matrix}\right.< =>\left\{{}\begin{matrix}x-2y=-5\\2x-y=-1\end{matrix}\right.< =>\left\{{}\begin{matrix}2x-4y=-10\\2x-y=-1\end{matrix}\right.< =>\left\{{}\begin{matrix}x-2y=-5\\-3y=-9\end{matrix}\right.< =>\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
TH2:
x<1 ==> x-1<0 ==>\(\left|x-1\right|=1-x\)
do đó ta có hpt\(\left\{{}\begin{matrix}x-2y=-5\\y=2-2x+3\end{matrix}\right.< =>}\left\{{}\begin{matrix}x-2y=-5\\y+2x=5\end{matrix}\right.< =>\left\{{}\begin{matrix}2x-4y=-10\\y+2x=5\end{matrix}\right.< =>\left\{{}\begin{matrix}x-2y=-5\\-5y=-15\end{matrix}\right.< =>\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

1. hiểu rồi k ngày đăng cầu mới--->trả lời ngay
2. chưa hiểu hỏi bải ngày--> nhận lời giải thích luôn
3.chưa k quay về câu 1

Làm mẫu 1 phần :
a) \(|3x-1|+|x-1|=4\left(1\right)\)
Ta có: \(3x-1=0\Leftrightarrow x=\frac{1}{3}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
3x-1 x-1 1/3 1 0 0 - - - + + + +
+) Với \(x< \frac{1}{3}\Rightarrow\hept{\begin{cases}3x-1< 0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=1-3x\\|x-1|=1-x\end{cases}\left(2\right)}}\)
Thay (2) vào (1) ta được :
\(\left(1-3x\right)+\left(1-x\right)=4\)
\(2-4x=4\)
\(4x=-2\)
\(x=\frac{-1}{2}\)( chọn )
+) Với \(\frac{1}{3}\le x< 1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(3x-1\right)+\left(1-x\right)=4\)
\(2x=4\)
\(x=2\)( chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1>0\end{cases}\Rightarrow}\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=x-1\end{cases}\left(4\right)}\)
Thay (4) vào (1) ta được :
\(\left(3x-1\right)+\left(x-1\right)=4\)
\(4x-2=4\)
\(4x=6\)
\(x=\frac{3}{2}\)( chọn )
Vậy \(x\in\left\{\frac{-1}{2};2;\frac{3}{2}\right\}\)

a: f(1)=-1,5
f(2)=-6
f(3)=-13,5
=>f(1)>f(2)>f(3)
b: \(f\left(-3\right)=-1,5\cdot9=-13,5\)
f(-2)=-1,5x4=-6
f(-1)=-1,5x1=-1,5
=>f(-3)<f(-2)<f(-1)
c: Hàm số này đồng biến khi x<0 và nghịch biến khi x>0
Của bạn thiếu dấu bằng .
Ta xét dấu các biểu thức trong dấu GTTĐ để khử dấu gttđ
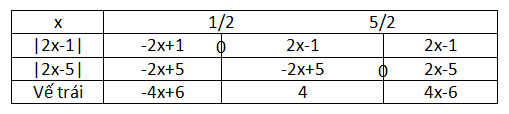
VD1: Giải pt:
|2x−1|+|2x−5|=4−−(1)|2x−1|+|2x−5|=4−−(1)
Giải:
Ta lập bảng khử dấu gttđ:
Từ đó ta xét 3 trường hợp sau:
- Xét x<12x<12
(1) trở thành −4x+6=4⇔x<12−4x+6=4⇔x<12, không phụ thuộc vào khoảng đang xét
- Xét 12≤x<5212≤x<52, (1) trở thành 4=44=4 đúng với mọi x khoảng đang xét
- Xét x≥52x≥52:
(1) trở thành 4x−6=4⇔x=524x−6=4⇔x=52, thuộc vào khoảng đang xét
Kết luận: Nghiệm của pt (1) là 12≤x≤5212≤x≤52
Mách nhỏ: Để khỏi nhầm lẫn trong việc lập bảng khử dấu giá trị tuyệt đối, các bạn hãy nhớ lấy câu: "Trái khác, phải cùng" tức là: Bên trái nghiệm của biểu thức sẽ mang dấu khác (trái) với biếu thức ta nhìn thấy, bên phải nghiệm của biểu thức sẽ mang dấu cùng với biểu thức ta nhìn thấy.
Phương pháp 2: Phương pháp biến đổi tương đương
Ta áp dụng 2 phép biến đổi cơ bản sau:
1) |a|=b⇔⎧⎪⎨⎪⎩b≥0[a=ba=−b|a|=b⇔{b≥0[a=ba=−b
2) |a|=|b|⇔[a=ba=−b|a|=|b|⇔[a=ba=−b
VD: Giải pt:
|x−1|=|3x−5|−(2)|x−1|=|3x−5|−(2)
Giải:
Áp dụng phép biến đổi 2 ta có:
(2)⇔[x−1=3x−5x−1=−3x+5(2)⇔[x−1=3x−5x−1=−3x+5
⇔⎡⎣x=2x=32⇔[x=2x=32
Kết luận: pt (2) có 2 nghiệm x1=2;x2=32x1=2;x2=32
Nhận xét: Ta có thể sử dụng phương pháp 1 để giải phương trình (2)