LH
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 4 2019
* tam giác đều
- chứng minh tam giác có 3 cạnh = nhau
- chứng minh tam giác có 3 góc = nhau
- chứng minh tam giác có 2 góc = 60*
- chứng minh tam giác cân có 1 góc = 60*
Có tổng cộng 4 cách nha
DT
6 tháng 4 2019
ngoài 4 cách ấy ra,đang còn một cách nx đó là:2 đường cao vừa là phân giác vừa là trung tuyến
học tốt!
4 tháng 5 2019
A B C D K M Q
a) b) cậu biết làm rồi nhé
c) Vì K là trung điểm cạnh BC ( gt )
\(\Rightarrow DK\)là trung tuyến cạnh BC.
Vì A là trung điểm của BD
\(\Rightarrow AC\)là trung tuyến cạnh BD
mà DK cắt AC tại M
\(\Rightarrow M\)là trọng tâm của tam giác BCD.
\(\Rightarrow MC=\frac{2}{3}AC\left(tc\right)\)
( BẠN TỰ THAY VÀO NHA )
4 tháng 5 2019
d) Vì tam giác BCD cân ( cmt )
\(\Rightarrow BC=DC\left(đn\right)\)
Mà AC là trung tuyến của tam giác BCD ( cmt )
\(\Rightarrow AC\)cũng là đường phân giác của góc BCD .( tc)
\(\Rightarrow\widehat{BCA}=\widehat{DCA}=\frac{1}{2}\widehat{BCD}\)
Xét tam giác BCM và tam giác DCM có:
\(\hept{\begin{cases}CMchung\\BC=CD\left(cmt\right)\\\widehat{BCA}=\widehat{DCA}\left(cmt\right)\end{cases}\Rightarrow\Delta BCM=\Delta DCM\left(c-g-c\right)}\)
\(\Rightarrow\hept{\begin{cases}BM=DM\left(2canht.ung\right)\left(1\right)\\\widehat{CBM}=\widehat{CDM}\left(2goct.ung\right)\end{cases}}\)
Xét tam giác BMK và tam giác DMQ có:
\(\hept{\begin{cases}BM=DM\left(cmt\right)\\\widehat{CDM}=\widehat{CBM}\left(cmt\right)\\\widehat{BMK}=\widehat{QMD}\left(2gocdoidinh\right)\end{cases}\Rightarrow\Delta BMK=\Delta DMQ\left(g-c-g\right)}\)
\(\Rightarrow MK=MQ\left(2canht.ung\right)\left(2\right)\)
Vì M là trọng tâm của tam giác BCD (cmt) (4)
mà DK là trung tuyến của tam giác BCD (cmt)
\(\Rightarrow DM=2.MK\left(tc\right)\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow BM=2.MQ\)
\(\Rightarrow BQ\)là trung tuyến của tam giác BCD (5)
Từ (4) và (5) \(\Rightarrow B,M,Q\)thẳng hàng
2T
28 tháng 8 2019
a) Vì hai đường tròn tâm A và B có bán kính bằng nhau nên AM = AN = BM = BN
Xét \(\Delta AMN\)và \(\Delta BMN\)
AM = BM (cmt)
AN = BN (cmt)
MN: cạnh chung
Suy ra \(\Delta AMN\)\(=\Delta BMN\left(c-c-c\right)\)
b) Gọi O là giao điểm của AB và MN
Dễ chứng minh được: \(\widehat{NAB}=\widehat{MBA}\)
Mà 2 góc này ở vị trí so le trong nên \(AN//BM\)
C/m: \(\Delta AON=\Delta BOM\left(g-c-g\right)\)
\(\Rightarrow OA=OB\)(hai cạnh tương ứng)
Sau đó c/m \(AB\perp MN\)suy ra MN là đường trung trực của AB
17 tháng 4 2019
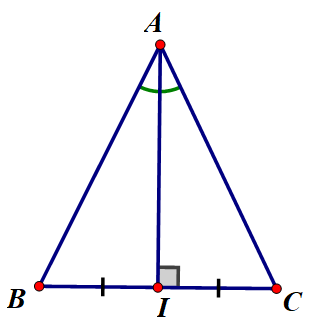
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
Tích chất đường trung trực. 1 điểm nằm trên đường trung trục thì cách đều 2 đầu mút của đoạn thẳng đó.
Thì tam giác cân luôn
Bài làm
Ví dụ: Cho tam giác ABC có nAH là đường trung trực. Chứng minh rằng: tam giác ABC cân tại A
A B C H
Bài làm
Xét tam giác ABC có:
AH là đường trung trực
=> AB = AC ( tính chất đường trung trực của một tam giác )
Do đó: Tam giác ABC cân tại A ( đpcm )
# Học tốt #